- Tap to switch levels
- Numbers
- Measurement
- Data Analysis
- Geometry
- Ratio and Percentage
- Speed
- Algebra
- Others
- Integration
SELECT A SUBJECT
- Numbers
Number Patterns
Question 1 of 303
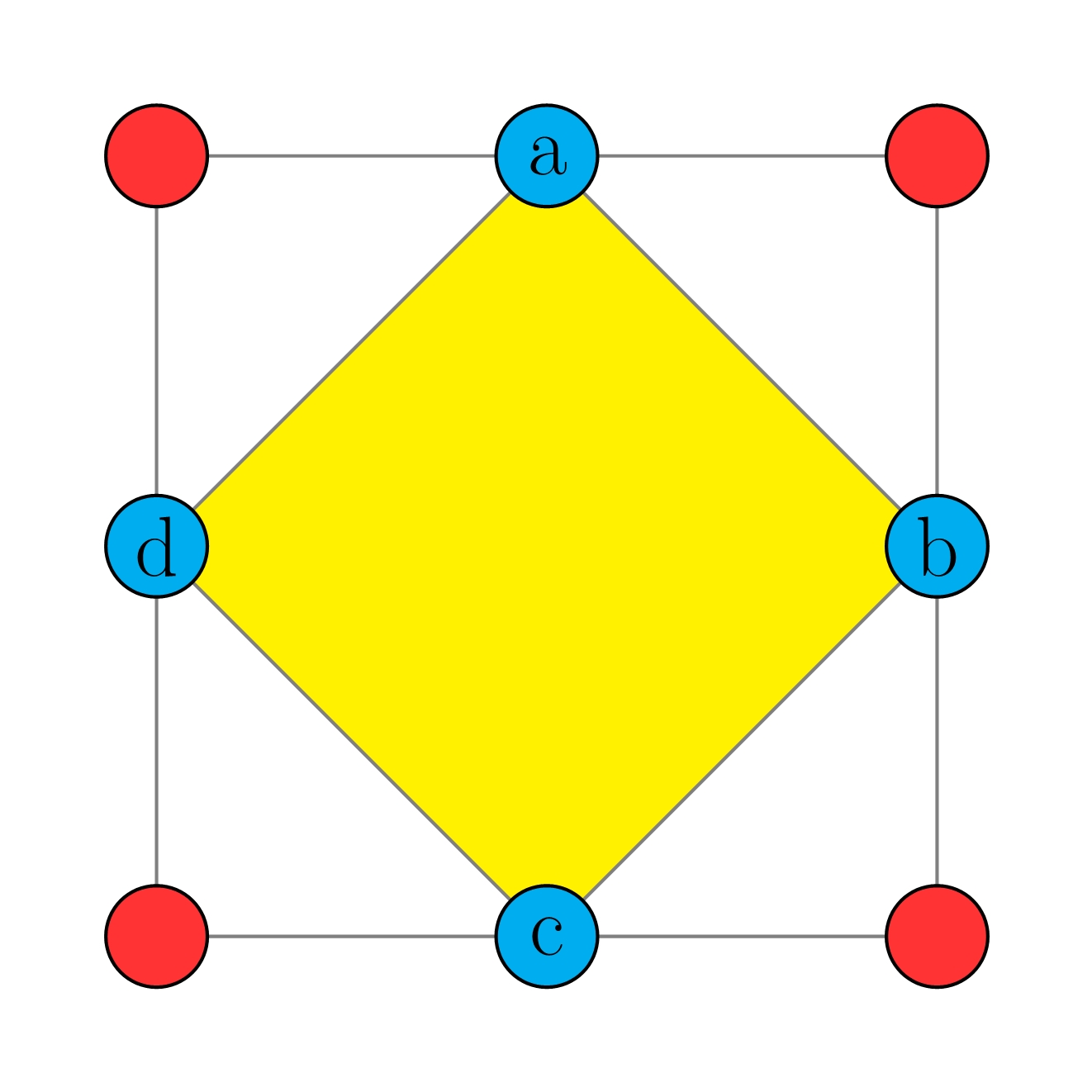
Mark fills in each circle with a number from $1$, $2$, $3$, $\dots$, $8$, such that the sum of numbers at all corners of any triangle is 12. Find $(a+b+c+d)$.
Select An Answer
Sorry. Please check the correct answer below.
Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 12\times 4 &= 48 \\ 1+2+3+\cdots + 7 &= 36 \\ 48-36 &= 12 \end{align*} Thus, $a+b+c+d=12$. Try, $1+2+3+6=12$
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 12\times 4 &= 48 \\ 1+2+3+\cdots + 7 &= 36 \\ 48-36 &= 12 \end{align*} Thus, $a+b+c+d=12$. Try, $1+2+3+6=12$
Find the remainder when the $2017^{\text{th}}$ term of the following sequence is divided by 5. \begin{equation} 1,\, 2,\, 4,\, 7,\, 11,\, 16,\, 22,\, 29,\, \dots \end{equation}
Select An Answer
Sorry. Please check the correct answer below.
Yay! Your are right.
Observe that pattern of remainders: \begin{equation} \begin{array}{ccccccccccc} n & 1 & 2 & 4 & 7 & 1 & 1 & 2 & 2 & 3 & 4 \\ & & & & & 1 & 6 & 2 & 9 & 7 & 6 \\\\ R & 1 & 2 & 4 & 2 & 1 & 1 & 2 & 4 & 2 & 1 \end{array} \end{equation} The pattern recurs: 1, 2, 4, 2, 1, $\dots$.
How many numbers are the same in both number patterns below? \begin{align*} 1,\ 3,\ 5,\ 7,\ 9,\ \dots ,\ 2015,\ 2017 \\ 1,\ 4,\ 7,\ 10,\ \dots ,\ 2014,\ 2017 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 7, 13, 19, 25, $\dots$ in both. Difference is 6 here, $(2\times 3 = 6)$. \begin{align*} (2017-1) \div 6 &= 336 \\ 336+1 &= 337 \end{align*}
Yay! Your are right.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 7, 13, 19, 25, $\dots$ in both. Difference is 6 here, $(2\times 3 = 6)$. \begin{align*} (2017-1) \div 6 &= 336 \\ 336+1 &= 337 \end{align*}
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 10. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 10\times 4 &= 40 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 40-36 &= 4 \end{align*} Thus, $a+b+c+d=4$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 10\times 4 &= 40 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 40-36 &= 4 \end{align*} Thus, $a+b+c+d=4$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 11. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 11\times 4 &= 44 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 44-36 &= 8 \end{align*} Thus, $a+b+c+d=8$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 11\times 4 &= 44 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 44-36 &= 8 \end{align*} Thus, $a+b+c+d=8$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 12. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 12\times 4 &= 48 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 48-36 &= 12 \end{align*} Thus, $a+b+c+d=12$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 12\times 4 &= 48 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 48-36 &= 12 \end{align*} Thus, $a+b+c+d=12$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 13. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 13\times 4 &= 52 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 52-36 &= 16 \end{align*} Thus, $a+b+c+d=16$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 13\times 4 &= 52 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 52-36 &= 16 \end{align*} Thus, $a+b+c+d=16$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 14. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 14\times 4 &= 56 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 56-36 &= 20 \end{align*} Thus, $a+b+c+d=20$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 14\times 4 &= 56 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 56-36 &= 20 \end{align*} Thus, $a+b+c+d=20$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 12. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 12\times 4 &= 48 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 48-36 &= 12 \end{align*} Thus, $a+b+c+d=12$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 12\times 4 &= 48 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 48-36 &= 12 \end{align*} Thus, $a+b+c+d=12$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 13. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 13\times 4 &= 52 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 52-36 &= 16 \end{align*} Thus, $a+b+c+d=16$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 13\times 4 &= 52 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 52-36 &= 16 \end{align*} Thus, $a+b+c+d=16$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 14. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 14\times 4 &= 56 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 56-36 &= 20 \end{align*} Thus, $a+b+c+d=20$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 14\times 4 &= 56 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 56-36 &= 20 \end{align*} Thus, $a+b+c+d=20$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 15. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 15\times 4 &= 60 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 60-36 &= 24 \end{align*} Thus, $a+b+c+d=24$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 15\times 4 &= 60 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 60-36 &= 24 \end{align*} Thus, $a+b+c+d=24$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 14. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 14\times 4 &= 56 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 56-36 &= 20 \end{align*} Thus, $a+b+c+d=20$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 14\times 4 &= 56 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 56-36 &= 20 \end{align*} Thus, $a+b+c+d=20$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 15. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 15\times 4 &= 60 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 60-36 &= 24 \end{align*} Thus, $a+b+c+d=24$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 15\times 4 &= 60 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 60-36 &= 24 \end{align*} Thus, $a+b+c+d=24$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 16. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 16\times 4 &= 64 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 64-36 &= 28 \end{align*} Thus, $a+b+c+d=28$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 16\times 4 &= 64 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 64-36 &= 28 \end{align*} Thus, $a+b+c+d=28$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 16. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 16\times 4 &= 64 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 64-36 &= 28 \end{align*} Thus, $a+b+c+d=28$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 16\times 4 &= 64 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 64-36 &= 28 \end{align*} Thus, $a+b+c+d=28$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 17. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 17\times 4 &= 68 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 68-36 &= 32 \end{align*} Thus, $a+b+c+d=32$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 17\times 4 &= 68 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 68-36 &= 32 \end{align*} Thus, $a+b+c+d=32$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 18. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 18\times 4 &= 72 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 72-36 &= 36 \end{align*} Thus, $a+b+c+d=36$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 18\times 4 &= 72 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 72-36 &= 36 \end{align*} Thus, $a+b+c+d=36$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 13. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 13\times 4 &= 52 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 52-36 &= 16 \end{align*} Thus, $a+b+c+d=16$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 13\times 4 &= 52 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 52-36 &= 16 \end{align*} Thus, $a+b+c+d=16$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 14. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 14\times 4 &= 56 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 56-36 &= 20 \end{align*} Thus, $a+b+c+d=20$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 14\times 4 &= 56 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 56-36 &= 20 \end{align*} Thus, $a+b+c+d=20$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 15. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 15\times 4 &= 60 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 60-36 &= 24 \end{align*} Thus, $a+b+c+d=24$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 15\times 4 &= 60 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 60-36 &= 24 \end{align*} Thus, $a+b+c+d=24$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 16. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 16\times 4 &= 64 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 64-36 &= 28 \end{align*} Thus, $a+b+c+d=28$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 16\times 4 &= 64 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 64-36 &= 28 \end{align*} Thus, $a+b+c+d=28$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 15. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 15\times 4 &= 60 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 60-36 &= 24 \end{align*} Thus, $a+b+c+d=24$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 15\times 4 &= 60 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 60-36 &= 24 \end{align*} Thus, $a+b+c+d=24$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 16. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 16\times 4 &= 64 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 64-36 &= 28 \end{align*} Thus, $a+b+c+d=28$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 16\times 4 &= 64 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 64-36 &= 28 \end{align*} Thus, $a+b+c+d=28$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 17. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 17\times 4 &= 68 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 68-36 &= 32 \end{align*} Thus, $a+b+c+d=32$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 17\times 4 &= 68 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 68-36 &= 32 \end{align*} Thus, $a+b+c+d=32$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 17. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 17\times 4 &= 68 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 68-36 &= 32 \end{align*} Thus, $a+b+c+d=32$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 17\times 4 &= 68 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 68-36 &= 32 \end{align*} Thus, $a+b+c+d=32$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 18. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 18\times 4 &= 72 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 72-36 &= 36 \end{align*} Thus, $a+b+c+d=36$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 18\times 4 &= 72 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 72-36 &= 36 \end{align*} Thus, $a+b+c+d=36$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 19. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 19\times 4 &= 76 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 76-36 &= 40 \end{align*} Thus, $a+b+c+d=40$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 19\times 4 &= 76 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 76-36 &= 40 \end{align*} Thus, $a+b+c+d=40$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 16. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 16\times 4 &= 64 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 64-36 &= 28 \end{align*} Thus, $a+b+c+d=28$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 16\times 4 &= 64 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 64-36 &= 28 \end{align*} Thus, $a+b+c+d=28$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 17. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 17\times 4 &= 68 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 68-36 &= 32 \end{align*} Thus, $a+b+c+d=32$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 17\times 4 &= 68 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 68-36 &= 32 \end{align*} Thus, $a+b+c+d=32$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 18. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 18\times 4 &= 72 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 72-36 &= 36 \end{align*} Thus, $a+b+c+d=36$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 18\times 4 &= 72 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 72-36 &= 36 \end{align*} Thus, $a+b+c+d=36$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 18. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 18\times 4 &= 72 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 72-36 &= 36 \end{align*} Thus, $a+b+c+d=36$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 18\times 4 &= 72 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 72-36 &= 36 \end{align*} Thus, $a+b+c+d=36$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 19. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 19\times 4 &= 76 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 76-36 &= 40 \end{align*} Thus, $a+b+c+d=40$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 19\times 4 &= 76 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 76-36 &= 40 \end{align*} Thus, $a+b+c+d=40$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 20. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 20\times 4 &= 80 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 80-36 &= 44 \end{align*} Thus, $a+b+c+d=44$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 20\times 4 &= 80 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 80-36 &= 44 \end{align*} Thus, $a+b+c+d=44$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 19. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 19\times 4 &= 76 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 76-36 &= 40 \end{align*} Thus, $a+b+c+d=40$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 19\times 4 &= 76 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 76-36 &= 40 \end{align*} Thus, $a+b+c+d=40$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 20. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 20\times 4 &= 80 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 80-36 &= 44 \end{align*} Thus, $a+b+c+d=44$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 20\times 4 &= 80 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 80-36 &= 44 \end{align*} Thus, $a+b+c+d=44$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 21. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 21\times 4 &= 84 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 84-36 &= 48 \end{align*} Thus, $a+b+c+d=48$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 21\times 4 &= 84 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 84-36 &= 48 \end{align*} Thus, $a+b+c+d=48$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 22. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 22\times 4 &= 88 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 88-36 &= 52 \end{align*} Thus, $a+b+c+d=52$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 22\times 4 &= 88 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 88-36 &= 52 \end{align*} Thus, $a+b+c+d=52$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 14. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 14\times 4 &= 56 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 56-36 &= 20 \end{align*} Thus, $a+b+c+d=20$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 14\times 4 &= 56 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 56-36 &= 20 \end{align*} Thus, $a+b+c+d=20$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 15. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 15\times 4 &= 60 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 60-36 &= 24 \end{align*} Thus, $a+b+c+d=24$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 15\times 4 &= 60 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 60-36 &= 24 \end{align*} Thus, $a+b+c+d=24$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 16. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 16\times 4 &= 64 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 64-36 &= 28 \end{align*} Thus, $a+b+c+d=28$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 16\times 4 &= 64 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 64-36 &= 28 \end{align*} Thus, $a+b+c+d=28$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 17. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 17\times 4 &= 68 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 68-36 &= 32 \end{align*} Thus, $a+b+c+d=32$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 17\times 4 &= 68 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 68-36 &= 32 \end{align*} Thus, $a+b+c+d=32$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 16. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 16\times 4 &= 64 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 64-36 &= 28 \end{align*} Thus, $a+b+c+d=28$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 16\times 4 &= 64 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 64-36 &= 28 \end{align*} Thus, $a+b+c+d=28$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 17. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 17\times 4 &= 68 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 68-36 &= 32 \end{align*} Thus, $a+b+c+d=32$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 17\times 4 &= 68 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 68-36 &= 32 \end{align*} Thus, $a+b+c+d=32$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 18. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 18\times 4 &= 72 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 72-36 &= 36 \end{align*} Thus, $a+b+c+d=36$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 18\times 4 &= 72 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 72-36 &= 36 \end{align*} Thus, $a+b+c+d=36$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 18. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 18\times 4 &= 72 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 72-36 &= 36 \end{align*} Thus, $a+b+c+d=36$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 18\times 4 &= 72 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 72-36 &= 36 \end{align*} Thus, $a+b+c+d=36$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 19. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 19\times 4 &= 76 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 76-36 &= 40 \end{align*} Thus, $a+b+c+d=40$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 19\times 4 &= 76 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 76-36 &= 40 \end{align*} Thus, $a+b+c+d=40$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 20. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 20\times 4 &= 80 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 80-36 &= 44 \end{align*} Thus, $a+b+c+d=44$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 20\times 4 &= 80 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 80-36 &= 44 \end{align*} Thus, $a+b+c+d=44$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 17. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 17\times 4 &= 68 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 68-36 &= 32 \end{align*} Thus, $a+b+c+d=32$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 17\times 4 &= 68 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 68-36 &= 32 \end{align*} Thus, $a+b+c+d=32$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 18. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 18\times 4 &= 72 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 72-36 &= 36 \end{align*} Thus, $a+b+c+d=36$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 18\times 4 &= 72 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 72-36 &= 36 \end{align*} Thus, $a+b+c+d=36$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 19. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 19\times 4 &= 76 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 76-36 &= 40 \end{align*} Thus, $a+b+c+d=40$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 19\times 4 &= 76 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 76-36 &= 40 \end{align*} Thus, $a+b+c+d=40$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 19. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 19\times 4 &= 76 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 76-36 &= 40 \end{align*} Thus, $a+b+c+d=40$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 19\times 4 &= 76 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 76-36 &= 40 \end{align*} Thus, $a+b+c+d=40$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 20. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 20\times 4 &= 80 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 80-36 &= 44 \end{align*} Thus, $a+b+c+d=44$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 20\times 4 &= 80 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 80-36 &= 44 \end{align*} Thus, $a+b+c+d=44$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 21. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 21\times 4 &= 84 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 84-36 &= 48 \end{align*} Thus, $a+b+c+d=48$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 21\times 4 &= 84 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 84-36 &= 48 \end{align*} Thus, $a+b+c+d=48$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 20. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 20\times 4 &= 80 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 80-36 &= 44 \end{align*} Thus, $a+b+c+d=44$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 20\times 4 &= 80 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 80-36 &= 44 \end{align*} Thus, $a+b+c+d=44$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 21. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 21\times 4 &= 84 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 84-36 &= 48 \end{align*} Thus, $a+b+c+d=48$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 21\times 4 &= 84 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 84-36 &= 48 \end{align*} Thus, $a+b+c+d=48$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 22. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 22\times 4 &= 88 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 88-36 &= 52 \end{align*} Thus, $a+b+c+d=52$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 22\times 4 &= 88 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 88-36 &= 52 \end{align*} Thus, $a+b+c+d=52$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 23. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 23\times 4 &= 92 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 92-36 &= 56 \end{align*} Thus, $a+b+c+d=56$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 23\times 4 &= 92 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 92-36 &= 56 \end{align*} Thus, $a+b+c+d=56$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 18. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 18\times 4 &= 72 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 72-36 &= 36 \end{align*} Thus, $a+b+c+d=36$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 18\times 4 &= 72 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 72-36 &= 36 \end{align*} Thus, $a+b+c+d=36$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 19. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 19\times 4 &= 76 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 76-36 &= 40 \end{align*} Thus, $a+b+c+d=40$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 19\times 4 &= 76 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 76-36 &= 40 \end{align*} Thus, $a+b+c+d=40$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 20. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 20\times 4 &= 80 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 80-36 &= 44 \end{align*} Thus, $a+b+c+d=44$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 20\times 4 &= 80 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 80-36 &= 44 \end{align*} Thus, $a+b+c+d=44$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 20. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 20\times 4 &= 80 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 80-36 &= 44 \end{align*} Thus, $a+b+c+d=44$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 20\times 4 &= 80 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 80-36 &= 44 \end{align*} Thus, $a+b+c+d=44$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 21. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 21\times 4 &= 84 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 84-36 &= 48 \end{align*} Thus, $a+b+c+d=48$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 21\times 4 &= 84 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 84-36 &= 48 \end{align*} Thus, $a+b+c+d=48$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 22. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 22\times 4 &= 88 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 88-36 &= 52 \end{align*} Thus, $a+b+c+d=52$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 22\times 4 &= 88 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 88-36 &= 52 \end{align*} Thus, $a+b+c+d=52$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 21. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 21\times 4 &= 84 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 84-36 &= 48 \end{align*} Thus, $a+b+c+d=48$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 21\times 4 &= 84 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 84-36 &= 48 \end{align*} Thus, $a+b+c+d=48$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 22. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 22\times 4 &= 88 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 88-36 &= 52 \end{align*} Thus, $a+b+c+d=52$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 22\times 4 &= 88 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 88-36 &= 52 \end{align*} Thus, $a+b+c+d=52$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 23. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 23\times 4 &= 92 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 92-36 &= 56 \end{align*} Thus, $a+b+c+d=56$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 23\times 4 &= 92 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 92-36 &= 56 \end{align*} Thus, $a+b+c+d=56$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 24. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 24\times 4 &= 96 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 96-36 &= 60 \end{align*} Thus, $a+b+c+d=60$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 24\times 4 &= 96 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 96-36 &= 60 \end{align*} Thus, $a+b+c+d=60$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 22. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 22\times 4 &= 88 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 88-36 &= 52 \end{align*} Thus, $a+b+c+d=52$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 22\times 4 &= 88 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 88-36 &= 52 \end{align*} Thus, $a+b+c+d=52$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 23. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 23\times 4 &= 92 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 92-36 &= 56 \end{align*} Thus, $a+b+c+d=56$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 23\times 4 &= 92 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 92-36 &= 56 \end{align*} Thus, $a+b+c+d=56$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 24. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 24\times 4 &= 96 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 96-36 &= 60 \end{align*} Thus, $a+b+c+d=60$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 24\times 4 &= 96 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 96-36 &= 60 \end{align*} Thus, $a+b+c+d=60$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 25. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 25\times 4 &= 100 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 100-36 &= 64 \end{align*} Thus, $a+b+c+d=64$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 25\times 4 &= 100 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 100-36 &= 64 \end{align*} Thus, $a+b+c+d=64$.
Mark fills in each circle with a number from $ 1 $, $ 2 $, $ 3 $, $\dots$, $ 8 $, such that the sum of numbers at all corners of any triangle is 26. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 26\times 4 &= 104 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 104-36 &= 68 \end{align*} Thus, $a+b+c+d=68$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 26\times 4 &= 104 \\ 1 + 2 + 3+\cdots + 8 &= 36 \\ 104-36 &= 68 \end{align*} Thus, $a+b+c+d=68$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 18. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 18\times 4 &= 72 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 72-64 &= 8 \end{align*} Thus, $a+b+c+d=8$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 18\times 4 &= 72 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 72-64 &= 8 \end{align*} Thus, $a+b+c+d=8$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 20. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 20\times 4 &= 80 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 80-64 &= 16 \end{align*} Thus, $a+b+c+d=16$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 20\times 4 &= 80 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 80-64 &= 16 \end{align*} Thus, $a+b+c+d=16$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 22. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 22\times 4 &= 88 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 88-64 &= 24 \end{align*} Thus, $a+b+c+d=24$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 22\times 4 &= 88 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 88-64 &= 24 \end{align*} Thus, $a+b+c+d=24$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 24. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 24\times 4 &= 96 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 96-64 &= 32 \end{align*} Thus, $a+b+c+d=32$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 24\times 4 &= 96 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 96-64 &= 32 \end{align*} Thus, $a+b+c+d=32$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 20. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 20\times 4 &= 80 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 80-64 &= 16 \end{align*} Thus, $a+b+c+d=16$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 20\times 4 &= 80 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 80-64 &= 16 \end{align*} Thus, $a+b+c+d=16$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 22. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 22\times 4 &= 88 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 88-64 &= 24 \end{align*} Thus, $a+b+c+d=24$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 22\times 4 &= 88 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 88-64 &= 24 \end{align*} Thus, $a+b+c+d=24$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 24. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 24\times 4 &= 96 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 96-64 &= 32 \end{align*} Thus, $a+b+c+d=32$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 24\times 4 &= 96 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 96-64 &= 32 \end{align*} Thus, $a+b+c+d=32$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 26. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 26\times 4 &= 104 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 104-64 &= 40 \end{align*} Thus, $a+b+c+d=40$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 26\times 4 &= 104 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 104-64 &= 40 \end{align*} Thus, $a+b+c+d=40$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 24. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 24\times 4 &= 96 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 96-64 &= 32 \end{align*} Thus, $a+b+c+d=32$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 24\times 4 &= 96 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 96-64 &= 32 \end{align*} Thus, $a+b+c+d=32$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 26. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 26\times 4 &= 104 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 104-64 &= 40 \end{align*} Thus, $a+b+c+d=40$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 26\times 4 &= 104 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 104-64 &= 40 \end{align*} Thus, $a+b+c+d=40$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 28. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 28\times 4 &= 112 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 112-64 &= 48 \end{align*} Thus, $a+b+c+d=48$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 28\times 4 &= 112 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 112-64 &= 48 \end{align*} Thus, $a+b+c+d=48$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 28. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 28\times 4 &= 112 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 112-64 &= 48 \end{align*} Thus, $a+b+c+d=48$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 28\times 4 &= 112 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 112-64 &= 48 \end{align*} Thus, $a+b+c+d=48$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 30. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 30\times 4 &= 120 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 120-64 &= 56 \end{align*} Thus, $a+b+c+d=56$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 30\times 4 &= 120 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 120-64 &= 56 \end{align*} Thus, $a+b+c+d=56$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 32. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 32\times 4 &= 128 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 128-64 &= 64 \end{align*} Thus, $a+b+c+d=64$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 32\times 4 &= 128 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 128-64 &= 64 \end{align*} Thus, $a+b+c+d=64$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 22. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 22\times 4 &= 88 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 88-64 &= 24 \end{align*} Thus, $a+b+c+d=24$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 22\times 4 &= 88 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 88-64 &= 24 \end{align*} Thus, $a+b+c+d=24$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 24. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 24\times 4 &= 96 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 96-64 &= 32 \end{align*} Thus, $a+b+c+d=32$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 24\times 4 &= 96 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 96-64 &= 32 \end{align*} Thus, $a+b+c+d=32$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 26. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 26\times 4 &= 104 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 104-64 &= 40 \end{align*} Thus, $a+b+c+d=40$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 26\times 4 &= 104 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 104-64 &= 40 \end{align*} Thus, $a+b+c+d=40$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 28. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 28\times 4 &= 112 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 112-64 &= 48 \end{align*} Thus, $a+b+c+d=48$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 28\times 4 &= 112 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 112-64 &= 48 \end{align*} Thus, $a+b+c+d=48$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 26. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 26\times 4 &= 104 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 104-64 &= 40 \end{align*} Thus, $a+b+c+d=40$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 26\times 4 &= 104 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 104-64 &= 40 \end{align*} Thus, $a+b+c+d=40$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 28. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 28\times 4 &= 112 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 112-64 &= 48 \end{align*} Thus, $a+b+c+d=48$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 28\times 4 &= 112 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 112-64 &= 48 \end{align*} Thus, $a+b+c+d=48$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 30. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 30\times 4 &= 120 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 120-64 &= 56 \end{align*} Thus, $a+b+c+d=56$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 30\times 4 &= 120 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 120-64 &= 56 \end{align*} Thus, $a+b+c+d=56$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 30. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 30\times 4 &= 120 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 120-64 &= 56 \end{align*} Thus, $a+b+c+d=56$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 30\times 4 &= 120 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 120-64 &= 56 \end{align*} Thus, $a+b+c+d=56$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 32. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 32\times 4 &= 128 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 128-64 &= 64 \end{align*} Thus, $a+b+c+d=64$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 32\times 4 &= 128 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 128-64 &= 64 \end{align*} Thus, $a+b+c+d=64$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 34. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 34\times 4 &= 136 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 136-64 &= 72 \end{align*} Thus, $a+b+c+d=72$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 34\times 4 &= 136 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 136-64 &= 72 \end{align*} Thus, $a+b+c+d=72$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 28. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 28\times 4 &= 112 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 112-64 &= 48 \end{align*} Thus, $a+b+c+d=48$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 28\times 4 &= 112 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 112-64 &= 48 \end{align*} Thus, $a+b+c+d=48$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 30. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 30\times 4 &= 120 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 120-64 &= 56 \end{align*} Thus, $a+b+c+d=56$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 30\times 4 &= 120 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 120-64 &= 56 \end{align*} Thus, $a+b+c+d=56$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 32. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 32\times 4 &= 128 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 128-64 &= 64 \end{align*} Thus, $a+b+c+d=64$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 32\times 4 &= 128 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 128-64 &= 64 \end{align*} Thus, $a+b+c+d=64$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 32. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 32\times 4 &= 128 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 128-64 &= 64 \end{align*} Thus, $a+b+c+d=64$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 32\times 4 &= 128 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 128-64 &= 64 \end{align*} Thus, $a+b+c+d=64$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 34. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 34\times 4 &= 136 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 136-64 &= 72 \end{align*} Thus, $a+b+c+d=72$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 34\times 4 &= 136 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 136-64 &= 72 \end{align*} Thus, $a+b+c+d=72$.
Mark fills in each circle with a number from $ 1 $, $ 3 $, $ 5 $, $\dots$, $ 15 $, such that the sum of numbers at all corners of any triangle is 36. Find $(a+b+c+d)$.

Select An Answer
Sorry. Please check the correct answer below.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 36\times 4 &= 144 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 144-64 &= 80 \end{align*} Thus, $a+b+c+d=80$.
Yay! Your are right.

Note: $a$, $b$, $c$ and $d$ are repeated when all triangles are added. \begin{align*} 36\times 4 &= 144 \\ 1 + 3 + 5+\cdots + 15 &= 64 \\ 144-64 &= 80 \end{align*} Thus, $a+b+c+d=80$.
Find the remainder when the $2015^{\text{th}}$ term of the following sequence is divided by 5. \begin{equation} 1,\,2,\,4,\,7,\,11,\,16,\,22,\,29,\,\dots \end{equation}
Select An Answer
Sorry. Please check the correct answer below.
Observe that pattern of remainders: \begin{equation} \begin{array}{ccccccccc} \text{number} & 1 & 2 & 4 & 7 & 11 & 16 & 22 & 29 \\\\ \text{remainder} & 1 & 2 & 4 & 2 & 1 & 1 & 2 & 4 \end{array} \end{equation} The pattern repeats at each 5 elements: \begin{equation} 1 , 2 , 4 , 2 , 1, 1 , 2, \cdots \end{equation} Because 2015 has remainder 0 when divided by the period size 5, it will have the same remainder as the 5th element in the sequence.
Yay! Your are right.
Observe that pattern of remainders: \begin{equation} \begin{array}{ccccccccc} \text{number} & 1 & 2 & 4 & 7 & 11 & 16 & 22 & 29 \\\\ \text{remainder} & 1 & 2 & 4 & 2 & 1 & 1 & 2 & 4 \end{array} \end{equation} The pattern repeats at each 5 elements: \begin{equation} 1 , 2 , 4 , 2 , 1, 1 , 2, \cdots \end{equation} Because 2015 has remainder 0 when divided by the period size 5, it will have the same remainder as the 5th element in the sequence.
Find the remainder when the $2017^{\text{th}}$ term of the following sequence is divided by 5. \begin{equation} 4,\,5,\,7,\,10,\,14,\,19,\,25,\,32,\,\dots \end{equation}
Select An Answer
Sorry. Please check the correct answer below.
Observe that pattern of remainders: \begin{equation} \begin{array}{ccccccccc} \text{number} & 4 & 5 & 7 & 10 & 14 & 19 & 25 & 32 \\\\ \text{remainder} & 4 & 0 & 2 & 0 & 4 & 4 & 0 & 2 \end{array} \end{equation} The pattern repeats at each 5 elements: \begin{equation} 4 , 0 , 2 , 0 , 4, 4 , 0, \cdots \end{equation} Because 2017 has remainder 2 when divided by the period size 5, it will have the same remainder as the 2th element in the sequence.
Yay! Your are right.
Observe that pattern of remainders: \begin{equation} \begin{array}{ccccccccc} \text{number} & 4 & 5 & 7 & 10 & 14 & 19 & 25 & 32 \\\\ \text{remainder} & 4 & 0 & 2 & 0 & 4 & 4 & 0 & 2 \end{array} \end{equation} The pattern repeats at each 5 elements: \begin{equation} 4 , 0 , 2 , 0 , 4, 4 , 0, \cdots \end{equation} Because 2017 has remainder 2 when divided by the period size 5, it will have the same remainder as the 2th element in the sequence.
Find the remainder when the $2019^{\text{th}}$ term of the following sequence is divided by 6. \begin{equation} 3,\,4,\,7,\,12,\,19,\,28,\,39,\,52,\,\dots \end{equation}
Select An Answer
Sorry. Please check the correct answer below.
Observe that pattern of remainders: \begin{equation} \begin{array}{ccccccccc} \text{number} & 3 & 4 & 7 & 12 & 19 & 28 & 39 & 52 \\\\ \text{remainder} & 3 & 4 & 1 & 0 & 1 & 4 & 3 & 4 \end{array} \end{equation} The pattern repeats at each 7 elements: \begin{equation} 3 , 4 , 1 , 0 , 1 , 4 , 3, 3 , 4, \cdots \end{equation} Because 2019 has remainder 3 when divided by the period size 7, it will have the same remainder as the 3th element in the sequence.
Yay! Your are right.
Observe that pattern of remainders: \begin{equation} \begin{array}{ccccccccc} \text{number} & 3 & 4 & 7 & 12 & 19 & 28 & 39 & 52 \\\\ \text{remainder} & 3 & 4 & 1 & 0 & 1 & 4 & 3 & 4 \end{array} \end{equation} The pattern repeats at each 7 elements: \begin{equation} 3 , 4 , 1 , 0 , 1 , 4 , 3, 3 , 4, \cdots \end{equation} Because 2019 has remainder 3 when divided by the period size 7, it will have the same remainder as the 3th element in the sequence.
Find the remainder when the $2015^{\text{th}}$ term of the following sequence is divided by 9. \begin{equation} 3,\,4,\,7,\,12,\,19,\,28,\,39,\,52,\,\dots \end{equation}
Select An Answer
Sorry. Please check the correct answer below.
Observe that pattern of remainders: \begin{equation} \begin{array}{ccccccccc} \text{number} & 3 & 4 & 7 & 12 & 19 & 28 & 39 & 52 \\\\ \text{remainder} & 3 & 4 & 7 & 3 & 1 & 1 & 3 & 7 \end{array} \end{equation} The pattern repeats at each 4 elements: \begin{equation} 3 , 4 , 7 , 3, 3 , 4, \cdots \end{equation} Because 2015 has remainder 3 when divided by the period size 4, it will have the same remainder as the 3th element in the sequence.
Yay! Your are right.
Observe that pattern of remainders: \begin{equation} \begin{array}{ccccccccc} \text{number} & 3 & 4 & 7 & 12 & 19 & 28 & 39 & 52 \\\\ \text{remainder} & 3 & 4 & 7 & 3 & 1 & 1 & 3 & 7 \end{array} \end{equation} The pattern repeats at each 4 elements: \begin{equation} 3 , 4 , 7 , 3, 3 , 4, \cdots \end{equation} Because 2015 has remainder 3 when divided by the period size 4, it will have the same remainder as the 3th element in the sequence.
Find the remainder when the $2017^{\text{th}}$ term of the following sequence is divided by 4. \begin{equation} 2,\,4,\,8,\,14,\,22,\,32,\,44,\,58,\,\dots \end{equation}
Select An Answer
Sorry. Please check the correct answer below.
Observe that pattern of remainders: \begin{equation} \begin{array}{ccccccccc} \text{number} & 2 & 4 & 8 & 14 & 22 & 32 & 44 & 58 \\\\ \text{remainder} & 2 & 0 & 0 & 2 & 2 & 0 & 0 & 2 \end{array} \end{equation} The pattern repeats at each 4 elements: \begin{equation} 2 , 0 , 0 , 2, 2 , 0, \cdots \end{equation} Because 2017 has remainder 1 when divided by the period size 4, it will have the same remainder as the 1th element in the sequence.
Yay! Your are right.
Observe that pattern of remainders: \begin{equation} \begin{array}{ccccccccc} \text{number} & 2 & 4 & 8 & 14 & 22 & 32 & 44 & 58 \\\\ \text{remainder} & 2 & 0 & 0 & 2 & 2 & 0 & 0 & 2 \end{array} \end{equation} The pattern repeats at each 4 elements: \begin{equation} 2 , 0 , 0 , 2, 2 , 0, \cdots \end{equation} Because 2017 has remainder 1 when divided by the period size 4, it will have the same remainder as the 1th element in the sequence.
Find the remainder when the $2019^{\text{th}}$ term of the following sequence is divided by 5. \begin{equation} 1,\,3,\,7,\,13,\,21,\,31,\,43,\,57,\,\dots \end{equation}
Select An Answer
Sorry. Please check the correct answer below.
Observe that pattern of remainders: \begin{equation} \begin{array}{ccccccccc} \text{number} & 1 & 3 & 7 & 13 & 21 & 31 & 43 & 57 \\\\ \text{remainder} & 1 & 3 & 2 & 3 & 1 & 1 & 3 & 2 \end{array} \end{equation} The pattern repeats at each 5 elements: \begin{equation} 1 , 3 , 2 , 3 , 1, 1 , 3, \cdots \end{equation} Because 2019 has remainder 4 when divided by the period size 5, it will have the same remainder as the 4th element in the sequence.
Yay! Your are right.
Observe that pattern of remainders: \begin{equation} \begin{array}{ccccccccc} \text{number} & 1 & 3 & 7 & 13 & 21 & 31 & 43 & 57 \\\\ \text{remainder} & 1 & 3 & 2 & 3 & 1 & 1 & 3 & 2 \end{array} \end{equation} The pattern repeats at each 5 elements: \begin{equation} 1 , 3 , 2 , 3 , 1, 1 , 3, \cdots \end{equation} Because 2019 has remainder 4 when divided by the period size 5, it will have the same remainder as the 4th element in the sequence.
Find the remainder when the $2015^{\text{th}}$ term of the following sequence is divided by 7. \begin{equation} 1,\,3,\,7,\,13,\,21,\,31,\,43,\,57,\,\dots \end{equation}
Select An Answer
Sorry. Please check the correct answer below.
Observe that pattern of remainders: \begin{equation} \begin{array}{ccccccccc} \text{number} & 1 & 3 & 7 & 13 & 21 & 31 & 43 & 57 \\\\ \text{remainder} & 1 & 3 & 0 & 6 & 0 & 3 & 1 & 1 \end{array} \end{equation} The pattern repeats at each 7 elements: \begin{equation} 1 , 3 , 0 , 6 , 0 , 3 , 1, 1 , 3, \cdots \end{equation} Because 2015 has remainder 6 when divided by the period size 7, it will have the same remainder as the 6th element in the sequence.
Yay! Your are right.
Observe that pattern of remainders: \begin{equation} \begin{array}{ccccccccc} \text{number} & 1 & 3 & 7 & 13 & 21 & 31 & 43 & 57 \\\\ \text{remainder} & 1 & 3 & 0 & 6 & 0 & 3 & 1 & 1 \end{array} \end{equation} The pattern repeats at each 7 elements: \begin{equation} 1 , 3 , 0 , 6 , 0 , 3 , 1, 1 , 3, \cdots \end{equation} Because 2015 has remainder 6 when divided by the period size 7, it will have the same remainder as the 6th element in the sequence.
Find the remainder when the $2017^{\text{th}}$ term of the following sequence is divided by 7. \begin{equation} 4,\,6,\,10,\,16,\,24,\,34,\,46,\,60,\,\dots \end{equation}
Select An Answer
Sorry. Please check the correct answer below.
Observe that pattern of remainders: \begin{equation} \begin{array}{ccccccccc} \text{number} & 4 & 6 & 10 & 16 & 24 & 34 & 46 & 60 \\\\ \text{remainder} & 4 & 6 & 3 & 2 & 3 & 6 & 4 & 4 \end{array} \end{equation} The pattern repeats at each 7 elements: \begin{equation} 4 , 6 , 3 , 2 , 3 , 6 , 4, 4 , 6, \cdots \end{equation} Because 2017 has remainder 1 when divided by the period size 7, it will have the same remainder as the 1th element in the sequence.
Yay! Your are right.
Observe that pattern of remainders: \begin{equation} \begin{array}{ccccccccc} \text{number} & 4 & 6 & 10 & 16 & 24 & 34 & 46 & 60 \\\\ \text{remainder} & 4 & 6 & 3 & 2 & 3 & 6 & 4 & 4 \end{array} \end{equation} The pattern repeats at each 7 elements: \begin{equation} 4 , 6 , 3 , 2 , 3 , 6 , 4, 4 , 6, \cdots \end{equation} Because 2017 has remainder 1 when divided by the period size 7, it will have the same remainder as the 1th element in the sequence.
Find the remainder when the $2019^{\text{th}}$ term of the following sequence is divided by 5. \begin{equation} 3,\,4,\,6,\,10,\,18,\,34,\,66,\,130,\,\dots \end{equation}
Select An Answer
Sorry. Please check the correct answer below.
Observe that pattern of remainders: \begin{equation} \begin{array}{ccccccccc} \text{number} & 3 & 4 & 6 & 10 & 18 & 34 & 66 & 130 \\\\ \text{remainder} & 3 & 4 & 1 & 0 & 3 & 4 & 1 & 0 \end{array} \end{equation} The pattern repeats at each 5 elements: \begin{equation} 3 , 4 , 1 , 0 , 3, 3 , 4, \cdots \end{equation} Because 2019 has remainder 4 when divided by the period size 5, it will have the same remainder as the 4th element in the sequence.
Yay! Your are right.
Observe that pattern of remainders: \begin{equation} \begin{array}{ccccccccc} \text{number} & 3 & 4 & 6 & 10 & 18 & 34 & 66 & 130 \\\\ \text{remainder} & 3 & 4 & 1 & 0 & 3 & 4 & 1 & 0 \end{array} \end{equation} The pattern repeats at each 5 elements: \begin{equation} 3 , 4 , 1 , 0 , 3, 3 , 4, \cdots \end{equation} Because 2019 has remainder 4 when divided by the period size 5, it will have the same remainder as the 4th element in the sequence.
Find the remainder when the $2015^{\text{th}}$ term of the following sequence is divided by 7. \begin{equation} 3,\,4,\,6,\,10,\,18,\,34,\,66,\,130,\,\dots \end{equation}
Select An Answer
Sorry. Please check the correct answer below.
Observe that pattern of remainders: \begin{equation} \begin{array}{ccccccccc} \text{number} & 3 & 4 & 6 & 10 & 18 & 34 & 66 & 130 \\\\ \text{remainder} & 3 & 4 & 6 & 3 & 4 & 6 & 3 & 4 \end{array} \end{equation} The pattern repeats at each 4 elements: \begin{equation} 3 , 4 , 6 , 3, 3 , 4, \cdots \end{equation} Because 2015 has remainder 3 when divided by the period size 4, it will have the same remainder as the 3th element in the sequence.
Yay! Your are right.
Observe that pattern of remainders: \begin{equation} \begin{array}{ccccccccc} \text{number} & 3 & 4 & 6 & 10 & 18 & 34 & 66 & 130 \\\\ \text{remainder} & 3 & 4 & 6 & 3 & 4 & 6 & 3 & 4 \end{array} \end{equation} The pattern repeats at each 4 elements: \begin{equation} 3 , 4 , 6 , 3, 3 , 4, \cdots \end{equation} Because 2015 has remainder 3 when divided by the period size 4, it will have the same remainder as the 3th element in the sequence.
How many numbers are the same in both number patterns below? \begin{align*} 1,\ 3,\ 5,\ 7,\ 9,\ & \dots ,\ 1859,\ 1861 \\ 1,\ 4,\ 7,\ 10,\ & \dots ,\ 1858,\ 1861 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 7, 13, 19, 25, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1861-1) \div 6 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 7, 13, 19, 25, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1861-1) \div 6 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 1,\ 3,\ 5,\ 7,\ 9,\ & \dots ,\ 1925,\ 1927 \\ 1,\ 4,\ 7,\ 10,\ & \dots ,\ 1924,\ 1927 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 7, 13, 19, 25, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1927-1) \div 6 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 7, 13, 19, 25, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1927-1) \div 6 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 1,\ 3,\ 5,\ 7,\ 9,\ & \dots ,\ 1991,\ 1993 \\ 1,\ 4,\ 7,\ 10,\ & \dots ,\ 1990,\ 1993 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 7, 13, 19, 25, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1993-1) \div 6 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 7, 13, 19, 25, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1993-1) \div 6 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 2,\ 4,\ 6,\ 8,\ 10,\ & \dots ,\ 1860,\ 1862 \\ 2,\ 5,\ 8,\ 11,\ & \dots ,\ 1859,\ 1862 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 8, 14, 20, 26, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1862-2) \div 6 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 8, 14, 20, 26, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1862-2) \div 6 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 2,\ 4,\ 6,\ 8,\ 10,\ & \dots ,\ 1926,\ 1928 \\ 2,\ 5,\ 8,\ 11,\ & \dots ,\ 1925,\ 1928 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 8, 14, 20, 26, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1928-2) \div 6 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 8, 14, 20, 26, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1928-2) \div 6 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 2,\ 4,\ 6,\ 8,\ 10,\ & \dots ,\ 1992,\ 1994 \\ 2,\ 5,\ 8,\ 11,\ & \dots ,\ 1991,\ 1994 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 8, 14, 20, 26, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1994-2) \div 6 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 8, 14, 20, 26, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1994-2) \div 6 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 3,\ 5,\ 7,\ 9,\ 11,\ & \dots ,\ 1861,\ 1863 \\ 3,\ 6,\ 9,\ 12,\ & \dots ,\ 1860,\ 1863 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 9, 15, 21, 27, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1863-3) \div 6 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 9, 15, 21, 27, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1863-3) \div 6 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 3,\ 5,\ 7,\ 9,\ 11,\ & \dots ,\ 1927,\ 1929 \\ 3,\ 6,\ 9,\ 12,\ & \dots ,\ 1926,\ 1929 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 9, 15, 21, 27, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1929-3) \div 6 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 9, 15, 21, 27, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1929-3) \div 6 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 3,\ 5,\ 7,\ 9,\ 11,\ & \dots ,\ 1993,\ 1995 \\ 3,\ 6,\ 9,\ 12,\ & \dots ,\ 1992,\ 1995 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 9, 15, 21, 27, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1995-3) \div 6 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 9, 15, 21, 27, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1995-3) \div 6 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 4,\ 6,\ 8,\ 10,\ 12,\ & \dots ,\ 1862,\ 1864 \\ 4,\ 7,\ 10,\ 13,\ & \dots ,\ 1861,\ 1864 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 10, 16, 22, 28, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1864-4) \div 6 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 10, 16, 22, 28, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1864-4) \div 6 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 4,\ 6,\ 8,\ 10,\ 12,\ & \dots ,\ 1928,\ 1930 \\ 4,\ 7,\ 10,\ 13,\ & \dots ,\ 1927,\ 1930 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 10, 16, 22, 28, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1930-4) \div 6 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 10, 16, 22, 28, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1930-4) \div 6 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 4,\ 6,\ 8,\ 10,\ 12,\ & \dots ,\ 1994,\ 1996 \\ 4,\ 7,\ 10,\ 13,\ & \dots ,\ 1993,\ 1996 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 10, 16, 22, 28, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1996-4) \div 6 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 10, 16, 22, 28, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1996-4) \div 6 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 5,\ 7,\ 9,\ 11,\ 13,\ & \dots ,\ 1863,\ 1865 \\ 5,\ 8,\ 11,\ 14,\ & \dots ,\ 1862,\ 1865 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 11, 17, 23, 29, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1865-5) \div 6 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 11, 17, 23, 29, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1865-5) \div 6 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 5,\ 7,\ 9,\ 11,\ 13,\ & \dots ,\ 1929,\ 1931 \\ 5,\ 8,\ 11,\ 14,\ & \dots ,\ 1928,\ 1931 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 11, 17, 23, 29, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1931-5) \div 6 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 11, 17, 23, 29, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1931-5) \div 6 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 5,\ 7,\ 9,\ 11,\ 13,\ & \dots ,\ 1995,\ 1997 \\ 5,\ 8,\ 11,\ 14,\ & \dots ,\ 1994,\ 1997 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 11, 17, 23, 29, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1997-5) \div 6 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 2 and 3 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 11, 17, 23, 29, $\dots$ in both. Difference is 6 here: $LCM(2, 3) = 6$. \begin{align*} (1997-5) \div 6 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 1,\ 3,\ 5,\ 7,\ 9,\ & \dots ,\ 1239,\ 1241 \\ 1,\ 5,\ 9,\ 13,\ & \dots ,\ 1237,\ 1241 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 5, 9, 13, 17, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1241-1) \div 4 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 5, 9, 13, 17, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1241-1) \div 4 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 1,\ 3,\ 5,\ 7,\ 9,\ & \dots ,\ 1283,\ 1285 \\ 1,\ 5,\ 9,\ 13,\ & \dots ,\ 1281,\ 1285 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 5, 9, 13, 17, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1285-1) \div 4 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 5, 9, 13, 17, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1285-1) \div 4 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 1,\ 3,\ 5,\ 7,\ 9,\ & \dots ,\ 1327,\ 1329 \\ 1,\ 5,\ 9,\ 13,\ & \dots ,\ 1325,\ 1329 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 5, 9, 13, 17, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1329-1) \div 4 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 5, 9, 13, 17, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1329-1) \div 4 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 2,\ 4,\ 6,\ 8,\ 10,\ & \dots ,\ 1240,\ 1242 \\ 2,\ 6,\ 10,\ 14,\ & \dots ,\ 1238,\ 1242 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 6, 10, 14, 18, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1242-2) \div 4 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 6, 10, 14, 18, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1242-2) \div 4 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 2,\ 4,\ 6,\ 8,\ 10,\ & \dots ,\ 1284,\ 1286 \\ 2,\ 6,\ 10,\ 14,\ & \dots ,\ 1282,\ 1286 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 6, 10, 14, 18, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1286-2) \div 4 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 6, 10, 14, 18, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1286-2) \div 4 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 2,\ 4,\ 6,\ 8,\ 10,\ & \dots ,\ 1328,\ 1330 \\ 2,\ 6,\ 10,\ 14,\ & \dots ,\ 1326,\ 1330 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 6, 10, 14, 18, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1330-2) \div 4 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 6, 10, 14, 18, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1330-2) \div 4 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 3,\ 5,\ 7,\ 9,\ 11,\ & \dots ,\ 1241,\ 1243 \\ 3,\ 7,\ 11,\ 15,\ & \dots ,\ 1239,\ 1243 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 7, 11, 15, 19, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1243-3) \div 4 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 7, 11, 15, 19, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1243-3) \div 4 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 3,\ 5,\ 7,\ 9,\ 11,\ & \dots ,\ 1285,\ 1287 \\ 3,\ 7,\ 11,\ 15,\ & \dots ,\ 1283,\ 1287 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 7, 11, 15, 19, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1287-3) \div 4 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 7, 11, 15, 19, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1287-3) \div 4 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 3,\ 5,\ 7,\ 9,\ 11,\ & \dots ,\ 1329,\ 1331 \\ 3,\ 7,\ 11,\ 15,\ & \dots ,\ 1327,\ 1331 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 7, 11, 15, 19, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1331-3) \div 4 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 7, 11, 15, 19, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1331-3) \div 4 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 4,\ 6,\ 8,\ 10,\ 12,\ & \dots ,\ 1242,\ 1244 \\ 4,\ 8,\ 12,\ 16,\ & \dots ,\ 1240,\ 1244 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 8, 12, 16, 20, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1244-4) \div 4 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 8, 12, 16, 20, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1244-4) \div 4 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 4,\ 6,\ 8,\ 10,\ 12,\ & \dots ,\ 1286,\ 1288 \\ 4,\ 8,\ 12,\ 16,\ & \dots ,\ 1284,\ 1288 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 8, 12, 16, 20, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1288-4) \div 4 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 8, 12, 16, 20, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1288-4) \div 4 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 4,\ 6,\ 8,\ 10,\ 12,\ & \dots ,\ 1330,\ 1332 \\ 4,\ 8,\ 12,\ 16,\ & \dots ,\ 1328,\ 1332 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 8, 12, 16, 20, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1332-4) \div 4 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 8, 12, 16, 20, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1332-4) \div 4 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 5,\ 7,\ 9,\ 11,\ 13,\ & \dots ,\ 1243,\ 1245 \\ 5,\ 9,\ 13,\ 17,\ & \dots ,\ 1241,\ 1245 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 9, 13, 17, 21, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1245-5) \div 4 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 9, 13, 17, 21, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1245-5) \div 4 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 5,\ 7,\ 9,\ 11,\ 13,\ & \dots ,\ 1287,\ 1289 \\ 5,\ 9,\ 13,\ 17,\ & \dots ,\ 1285,\ 1289 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 9, 13, 17, 21, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1289-5) \div 4 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 9, 13, 17, 21, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1289-5) \div 4 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 5,\ 7,\ 9,\ 11,\ 13,\ & \dots ,\ 1331,\ 1333 \\ 5,\ 9,\ 13,\ 17,\ & \dots ,\ 1329,\ 1333 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 9, 13, 17, 21, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1333-5) \div 4 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 2 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 9, 13, 17, 21, $\dots$ in both. Difference is 4 here: $LCM(2, 4) = 4$. \begin{align*} (1333-5) \div 4 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 1,\ 3,\ 5,\ 7,\ 9,\ & \dots ,\ 3099,\ 3101 \\ 1,\ 6,\ 11,\ 16,\ & \dots ,\ 3096,\ 3101 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 11, 21, 31, 41, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3101-1) \div 10 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 11, 21, 31, 41, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3101-1) \div 10 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 1,\ 3,\ 5,\ 7,\ 9,\ & \dots ,\ 3209,\ 3211 \\ 1,\ 6,\ 11,\ 16,\ & \dots ,\ 3206,\ 3211 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 11, 21, 31, 41, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3211-1) \div 10 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 11, 21, 31, 41, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3211-1) \div 10 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 1,\ 3,\ 5,\ 7,\ 9,\ & \dots ,\ 3319,\ 3321 \\ 1,\ 6,\ 11,\ 16,\ & \dots ,\ 3316,\ 3321 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 11, 21, 31, 41, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3321-1) \div 10 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 11, 21, 31, 41, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3321-1) \div 10 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 2,\ 4,\ 6,\ 8,\ 10,\ & \dots ,\ 3100,\ 3102 \\ 2,\ 7,\ 12,\ 17,\ & \dots ,\ 3097,\ 3102 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 12, 22, 32, 42, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3102-2) \div 10 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 12, 22, 32, 42, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3102-2) \div 10 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 2,\ 4,\ 6,\ 8,\ 10,\ & \dots ,\ 3210,\ 3212 \\ 2,\ 7,\ 12,\ 17,\ & \dots ,\ 3207,\ 3212 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 12, 22, 32, 42, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3212-2) \div 10 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 12, 22, 32, 42, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3212-2) \div 10 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 2,\ 4,\ 6,\ 8,\ 10,\ & \dots ,\ 3320,\ 3322 \\ 2,\ 7,\ 12,\ 17,\ & \dots ,\ 3317,\ 3322 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 12, 22, 32, 42, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3322-2) \div 10 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 12, 22, 32, 42, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3322-2) \div 10 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 3,\ 5,\ 7,\ 9,\ 11,\ & \dots ,\ 3101,\ 3103 \\ 3,\ 8,\ 13,\ 18,\ & \dots ,\ 3098,\ 3103 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 13, 23, 33, 43, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3103-3) \div 10 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 13, 23, 33, 43, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3103-3) \div 10 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 3,\ 5,\ 7,\ 9,\ 11,\ & \dots ,\ 3211,\ 3213 \\ 3,\ 8,\ 13,\ 18,\ & \dots ,\ 3208,\ 3213 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 13, 23, 33, 43, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3213-3) \div 10 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 13, 23, 33, 43, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3213-3) \div 10 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 3,\ 5,\ 7,\ 9,\ 11,\ & \dots ,\ 3321,\ 3323 \\ 3,\ 8,\ 13,\ 18,\ & \dots ,\ 3318,\ 3323 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 13, 23, 33, 43, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3323-3) \div 10 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 13, 23, 33, 43, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3323-3) \div 10 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 4,\ 6,\ 8,\ 10,\ 12,\ & \dots ,\ 3102,\ 3104 \\ 4,\ 9,\ 14,\ 19,\ & \dots ,\ 3099,\ 3104 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 14, 24, 34, 44, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3104-4) \div 10 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 14, 24, 34, 44, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3104-4) \div 10 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 4,\ 6,\ 8,\ 10,\ 12,\ & \dots ,\ 3212,\ 3214 \\ 4,\ 9,\ 14,\ 19,\ & \dots ,\ 3209,\ 3214 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 14, 24, 34, 44, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3214-4) \div 10 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 14, 24, 34, 44, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3214-4) \div 10 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 4,\ 6,\ 8,\ 10,\ 12,\ & \dots ,\ 3322,\ 3324 \\ 4,\ 9,\ 14,\ 19,\ & \dots ,\ 3319,\ 3324 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 14, 24, 34, 44, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3324-4) \div 10 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 14, 24, 34, 44, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3324-4) \div 10 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 5,\ 7,\ 9,\ 11,\ 13,\ & \dots ,\ 3103,\ 3105 \\ 5,\ 10,\ 15,\ 20,\ & \dots ,\ 3100,\ 3105 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 15, 25, 35, 45, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3105-5) \div 10 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 15, 25, 35, 45, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3105-5) \div 10 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 5,\ 7,\ 9,\ 11,\ 13,\ & \dots ,\ 3213,\ 3215 \\ 5,\ 10,\ 15,\ 20,\ & \dots ,\ 3210,\ 3215 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 15, 25, 35, 45, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3215-5) \div 10 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 15, 25, 35, 45, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3215-5) \div 10 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 5,\ 7,\ 9,\ 11,\ 13,\ & \dots ,\ 3323,\ 3325 \\ 5,\ 10,\ 15,\ 20,\ & \dots ,\ 3320,\ 3325 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 15, 25, 35, 45, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3325-5) \div 10 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 2 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 15, 25, 35, 45, $\dots$ in both. Difference is 10 here: $LCM(2, 5) = 10$. \begin{align*} (3325-5) \div 10 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 1,\ 4,\ 7,\ 10,\ 13,\ & \dots ,\ 3718,\ 3721 \\ 1,\ 5,\ 9,\ 13,\ & \dots ,\ 3717,\ 3721 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 13, 25, 37, 49, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3721-1) \div 12 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 13, 25, 37, 49, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3721-1) \div 12 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 1,\ 4,\ 7,\ 10,\ 13,\ & \dots ,\ 3850,\ 3853 \\ 1,\ 5,\ 9,\ 13,\ & \dots ,\ 3849,\ 3853 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 13, 25, 37, 49, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3853-1) \div 12 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 13, 25, 37, 49, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3853-1) \div 12 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 1,\ 4,\ 7,\ 10,\ 13,\ & \dots ,\ 3982,\ 3985 \\ 1,\ 5,\ 9,\ 13,\ & \dots ,\ 3981,\ 3985 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 13, 25, 37, 49, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3985-1) \div 12 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 13, 25, 37, 49, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3985-1) \div 12 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 2,\ 5,\ 8,\ 11,\ 14,\ & \dots ,\ 3719,\ 3722 \\ 2,\ 6,\ 10,\ 14,\ & \dots ,\ 3718,\ 3722 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 14, 26, 38, 50, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3722-2) \div 12 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 14, 26, 38, 50, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3722-2) \div 12 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 2,\ 5,\ 8,\ 11,\ 14,\ & \dots ,\ 3851,\ 3854 \\ 2,\ 6,\ 10,\ 14,\ & \dots ,\ 3850,\ 3854 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 14, 26, 38, 50, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3854-2) \div 12 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 14, 26, 38, 50, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3854-2) \div 12 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 2,\ 5,\ 8,\ 11,\ 14,\ & \dots ,\ 3983,\ 3986 \\ 2,\ 6,\ 10,\ 14,\ & \dots ,\ 3982,\ 3986 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 14, 26, 38, 50, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3986-2) \div 12 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 14, 26, 38, 50, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3986-2) \div 12 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 3,\ 6,\ 9,\ 12,\ 15,\ & \dots ,\ 3720,\ 3723 \\ 3,\ 7,\ 11,\ 15,\ & \dots ,\ 3719,\ 3723 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 15, 27, 39, 51, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3723-3) \div 12 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 15, 27, 39, 51, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3723-3) \div 12 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 3,\ 6,\ 9,\ 12,\ 15,\ & \dots ,\ 3852,\ 3855 \\ 3,\ 7,\ 11,\ 15,\ & \dots ,\ 3851,\ 3855 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 15, 27, 39, 51, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3855-3) \div 12 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 15, 27, 39, 51, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3855-3) \div 12 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 3,\ 6,\ 9,\ 12,\ 15,\ & \dots ,\ 3984,\ 3987 \\ 3,\ 7,\ 11,\ 15,\ & \dots ,\ 3983,\ 3987 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 15, 27, 39, 51, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3987-3) \div 12 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 15, 27, 39, 51, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3987-3) \div 12 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 4,\ 7,\ 10,\ 13,\ 16,\ & \dots ,\ 3721,\ 3724 \\ 4,\ 8,\ 12,\ 16,\ & \dots ,\ 3720,\ 3724 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 16, 28, 40, 52, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3724-4) \div 12 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 16, 28, 40, 52, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3724-4) \div 12 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 4,\ 7,\ 10,\ 13,\ 16,\ & \dots ,\ 3853,\ 3856 \\ 4,\ 8,\ 12,\ 16,\ & \dots ,\ 3852,\ 3856 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 16, 28, 40, 52, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3856-4) \div 12 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 16, 28, 40, 52, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3856-4) \div 12 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 4,\ 7,\ 10,\ 13,\ 16,\ & \dots ,\ 3985,\ 3988 \\ 4,\ 8,\ 12,\ 16,\ & \dots ,\ 3984,\ 3988 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 16, 28, 40, 52, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3988-4) \div 12 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 16, 28, 40, 52, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3988-4) \div 12 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 5,\ 8,\ 11,\ 14,\ 17,\ & \dots ,\ 3722,\ 3725 \\ 5,\ 9,\ 13,\ 17,\ & \dots ,\ 3721,\ 3725 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 17, 29, 41, 53, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3725-5) \div 12 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 17, 29, 41, 53, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3725-5) \div 12 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 5,\ 8,\ 11,\ 14,\ 17,\ & \dots ,\ 3854,\ 3857 \\ 5,\ 9,\ 13,\ 17,\ & \dots ,\ 3853,\ 3857 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 17, 29, 41, 53, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3857-5) \div 12 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 17, 29, 41, 53, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3857-5) \div 12 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 5,\ 8,\ 11,\ 14,\ 17,\ & \dots ,\ 3986,\ 3989 \\ 5,\ 9,\ 13,\ 17,\ & \dots ,\ 3985,\ 3989 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 17, 29, 41, 53, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3989-5) \div 12 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 3 and 4 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 17, 29, 41, 53, $\dots$ in both. Difference is 12 here: $LCM(3, 4) = 12$. \begin{align*} (3989-5) \div 12 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 1,\ 4,\ 7,\ 10,\ 13,\ & \dots ,\ 4648,\ 4651 \\ 1,\ 6,\ 11,\ 16,\ & \dots ,\ 4646,\ 4651 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 16, 31, 46, 61, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4651-1) \div 15 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 16, 31, 46, 61, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4651-1) \div 15 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 1,\ 4,\ 7,\ 10,\ 13,\ & \dots ,\ 4813,\ 4816 \\ 1,\ 6,\ 11,\ 16,\ & \dots ,\ 4811,\ 4816 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 16, 31, 46, 61, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4816-1) \div 15 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 16, 31, 46, 61, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4816-1) \div 15 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 1,\ 4,\ 7,\ 10,\ 13,\ & \dots ,\ 4978,\ 4981 \\ 1,\ 6,\ 11,\ 16,\ & \dots ,\ 4976,\ 4981 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 16, 31, 46, 61, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4981-1) \div 15 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 16, 31, 46, 61, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4981-1) \div 15 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 2,\ 5,\ 8,\ 11,\ 14,\ & \dots ,\ 4649,\ 4652 \\ 2,\ 7,\ 12,\ 17,\ & \dots ,\ 4647,\ 4652 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 17, 32, 47, 62, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4652-2) \div 15 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 17, 32, 47, 62, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4652-2) \div 15 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 2,\ 5,\ 8,\ 11,\ 14,\ & \dots ,\ 4814,\ 4817 \\ 2,\ 7,\ 12,\ 17,\ & \dots ,\ 4812,\ 4817 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 17, 32, 47, 62, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4817-2) \div 15 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 17, 32, 47, 62, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4817-2) \div 15 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 2,\ 5,\ 8,\ 11,\ 14,\ & \dots ,\ 4979,\ 4982 \\ 2,\ 7,\ 12,\ 17,\ & \dots ,\ 4977,\ 4982 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 17, 32, 47, 62, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4982-2) \div 15 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 17, 32, 47, 62, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4982-2) \div 15 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 3,\ 6,\ 9,\ 12,\ 15,\ & \dots ,\ 4650,\ 4653 \\ 3,\ 8,\ 13,\ 18,\ & \dots ,\ 4648,\ 4653 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 18, 33, 48, 63, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4653-3) \div 15 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 18, 33, 48, 63, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4653-3) \div 15 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 3,\ 6,\ 9,\ 12,\ 15,\ & \dots ,\ 4815,\ 4818 \\ 3,\ 8,\ 13,\ 18,\ & \dots ,\ 4813,\ 4818 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 18, 33, 48, 63, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4818-3) \div 15 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 18, 33, 48, 63, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4818-3) \div 15 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 3,\ 6,\ 9,\ 12,\ 15,\ & \dots ,\ 4980,\ 4983 \\ 3,\ 8,\ 13,\ 18,\ & \dots ,\ 4978,\ 4983 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 18, 33, 48, 63, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4983-3) \div 15 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 18, 33, 48, 63, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4983-3) \div 15 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 4,\ 7,\ 10,\ 13,\ 16,\ & \dots ,\ 4651,\ 4654 \\ 4,\ 9,\ 14,\ 19,\ & \dots ,\ 4649,\ 4654 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 19, 34, 49, 64, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4654-4) \div 15 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 19, 34, 49, 64, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4654-4) \div 15 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 4,\ 7,\ 10,\ 13,\ 16,\ & \dots ,\ 4816,\ 4819 \\ 4,\ 9,\ 14,\ 19,\ & \dots ,\ 4814,\ 4819 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 19, 34, 49, 64, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4819-4) \div 15 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 19, 34, 49, 64, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4819-4) \div 15 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 4,\ 7,\ 10,\ 13,\ 16,\ & \dots ,\ 4981,\ 4984 \\ 4,\ 9,\ 14,\ 19,\ & \dots ,\ 4979,\ 4984 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 19, 34, 49, 64, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4984-4) \div 15 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 19, 34, 49, 64, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4984-4) \div 15 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 5,\ 8,\ 11,\ 14,\ 17,\ & \dots ,\ 4652,\ 4655 \\ 5,\ 10,\ 15,\ 20,\ & \dots ,\ 4650,\ 4655 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 20, 35, 50, 65, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4655-5) \div 15 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 20, 35, 50, 65, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4655-5) \div 15 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 5,\ 8,\ 11,\ 14,\ 17,\ & \dots ,\ 4817,\ 4820 \\ 5,\ 10,\ 15,\ 20,\ & \dots ,\ 4815,\ 4820 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 20, 35, 50, 65, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4820-5) \div 15 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 20, 35, 50, 65, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4820-5) \div 15 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 5,\ 8,\ 11,\ 14,\ 17,\ & \dots ,\ 4982,\ 4985 \\ 5,\ 10,\ 15,\ 20,\ & \dots ,\ 4980,\ 4985 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 20, 35, 50, 65, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4985-5) \div 15 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 3 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 20, 35, 50, 65, $\dots$ in both. Difference is 15 here: $LCM(3, 5) = 15$. \begin{align*} (4985-5) \div 15 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 1,\ 5,\ 9,\ 13,\ 17,\ & \dots ,\ 6197,\ 6201 \\ 1,\ 6,\ 11,\ 16,\ & \dots ,\ 6196,\ 6201 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 21, 41, 61, 81, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6201-1) \div 20 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 21, 41, 61, 81, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6201-1) \div 20 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 1,\ 5,\ 9,\ 13,\ 17,\ & \dots ,\ 6417,\ 6421 \\ 1,\ 6,\ 11,\ 16,\ & \dots ,\ 6416,\ 6421 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 21, 41, 61, 81, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6421-1) \div 20 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 21, 41, 61, 81, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6421-1) \div 20 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 1,\ 5,\ 9,\ 13,\ 17,\ & \dots ,\ 6637,\ 6641 \\ 1,\ 6,\ 11,\ 16,\ & \dots ,\ 6636,\ 6641 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 21, 41, 61, 81, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6641-1) \div 20 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 1, 21, 41, 61, 81, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6641-1) \div 20 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 2,\ 6,\ 10,\ 14,\ 18,\ & \dots ,\ 6198,\ 6202 \\ 2,\ 7,\ 12,\ 17,\ & \dots ,\ 6197,\ 6202 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 22, 42, 62, 82, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6202-2) \div 20 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 22, 42, 62, 82, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6202-2) \div 20 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 2,\ 6,\ 10,\ 14,\ 18,\ & \dots ,\ 6418,\ 6422 \\ 2,\ 7,\ 12,\ 17,\ & \dots ,\ 6417,\ 6422 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 22, 42, 62, 82, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6422-2) \div 20 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 22, 42, 62, 82, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6422-2) \div 20 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 2,\ 6,\ 10,\ 14,\ 18,\ & \dots ,\ 6638,\ 6642 \\ 2,\ 7,\ 12,\ 17,\ & \dots ,\ 6637,\ 6642 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 22, 42, 62, 82, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6642-2) \div 20 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 2, 22, 42, 62, 82, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6642-2) \div 20 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 3,\ 7,\ 11,\ 15,\ 19,\ & \dots ,\ 6199,\ 6203 \\ 3,\ 8,\ 13,\ 18,\ & \dots ,\ 6198,\ 6203 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 23, 43, 63, 83, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6203-3) \div 20 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 23, 43, 63, 83, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6203-3) \div 20 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 3,\ 7,\ 11,\ 15,\ 19,\ & \dots ,\ 6419,\ 6423 \\ 3,\ 8,\ 13,\ 18,\ & \dots ,\ 6418,\ 6423 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 23, 43, 63, 83, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6423-3) \div 20 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 23, 43, 63, 83, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6423-3) \div 20 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 3,\ 7,\ 11,\ 15,\ 19,\ & \dots ,\ 6639,\ 6643 \\ 3,\ 8,\ 13,\ 18,\ & \dots ,\ 6638,\ 6643 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 23, 43, 63, 83, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6643-3) \div 20 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 3, 23, 43, 63, 83, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6643-3) \div 20 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 4,\ 8,\ 12,\ 16,\ 20,\ & \dots ,\ 6200,\ 6204 \\ 4,\ 9,\ 14,\ 19,\ & \dots ,\ 6199,\ 6204 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 24, 44, 64, 84, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6204-4) \div 20 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 24, 44, 64, 84, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6204-4) \div 20 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 4,\ 8,\ 12,\ 16,\ 20,\ & \dots ,\ 6420,\ 6424 \\ 4,\ 9,\ 14,\ 19,\ & \dots ,\ 6419,\ 6424 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 24, 44, 64, 84, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6424-4) \div 20 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 24, 44, 64, 84, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6424-4) \div 20 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 4,\ 8,\ 12,\ 16,\ 20,\ & \dots ,\ 6640,\ 6644 \\ 4,\ 9,\ 14,\ 19,\ & \dots ,\ 6639,\ 6644 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 24, 44, 64, 84, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6644-4) \div 20 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 4, 24, 44, 64, 84, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6644-4) \div 20 &= 332 \\ 332+1 &= 333 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 5,\ 9,\ 13,\ 17,\ 21,\ & \dots ,\ 6201,\ 6205 \\ 5,\ 10,\ 15,\ 20,\ & \dots ,\ 6200,\ 6205 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 25, 45, 65, 85, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6205-5) \div 20 &= 310 \\ 310+1 &= 311 \end{align*}
Yay! Your are right.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 25, 45, 65, 85, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6205-5) \div 20 &= 310 \\ 310+1 &= 311 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 5,\ 9,\ 13,\ 17,\ 21,\ & \dots ,\ 6421,\ 6425 \\ 5,\ 10,\ 15,\ 20,\ & \dots ,\ 6420,\ 6425 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 25, 45, 65, 85, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6425-5) \div 20 &= 321 \\ 321+1 &= 322 \end{align*}
Yay! Your are right.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 25, 45, 65, 85, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6425-5) \div 20 &= 321 \\ 321+1 &= 322 \end{align*}
How many numbers are the same in both number patterns below? \begin{align*} 5,\ 9,\ 13,\ 17,\ 21,\ & \dots ,\ 6641,\ 6645 \\ 5,\ 10,\ 15,\ 20,\ & \dots ,\ 6640,\ 6645 \\ \end{align*}
Select An Answer
Sorry. Please check the correct answer below.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 25, 45, 65, 85, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6645-5) \div 20 &= 332 \\ 332+1 &= 333 \end{align*}
Yay! Your are right.
Differences are 4 and 5 in $1^{\text{st}}$ and $2^{\text{nd}}$ sequences respectively. We are looking for 5, 25, 45, 65, 85, $\dots$ in both. Difference is 20 here: $LCM(4, 5) = 20$. \begin{align*} (6645-5) \div 20 &= 332 \\ 332+1 &= 333 \end{align*}
1903 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1903 \div 4 &= 475 \text{R} 3 \\ 1903 \div 3 &= 634 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1903 \div 12 = 158 \text{R} 7 \end{equation} So, $158\times 3 = 474$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $474+2=476$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1903 \div 4 &= 475 \text{R} 3 \\ 1903 \div 3 &= 634 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1903 \div 12 = 158 \text{R} 7 \end{equation} So, $158\times 3 = 474$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $474+2=476$
1909 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1909 \div 4 &= 477 \text{R} 1 \\ 1909 \div 3 &= 636 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1909 \div 12 = 159 \text{R} 1 \end{equation} So, $159\times 3 = 477$. But the last soldier had the same number both times. So, $477+1=478$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1909 \div 4 &= 477 \text{R} 1 \\ 1909 \div 3 &= 636 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1909 \div 12 = 159 \text{R} 1 \end{equation} So, $159\times 3 = 477$. But the last soldier had the same number both times. So, $477+1=478$
1915 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1915 \div 4 &= 478 \text{R} 3 \\ 1915 \div 3 &= 638 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1915 \div 12 = 159 \text{R} 7 \end{equation} So, $159\times 3 = 477$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $477+2=479$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1915 \div 4 &= 478 \text{R} 3 \\ 1915 \div 3 &= 638 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1915 \div 12 = 159 \text{R} 7 \end{equation} So, $159\times 3 = 477$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $477+2=479$
1921 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1921 \div 4 &= 480 \text{R} 1 \\ 1921 \div 3 &= 640 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1921 \div 12 = 160 \text{R} 1 \end{equation} So, $160\times 3 = 480$. But the last soldier had the same number both times. So, $480+1=481$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1921 \div 4 &= 480 \text{R} 1 \\ 1921 \div 3 &= 640 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1921 \div 12 = 160 \text{R} 1 \end{equation} So, $160\times 3 = 480$. But the last soldier had the same number both times. So, $480+1=481$
1927 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1927 \div 4 &= 481 \text{R} 3 \\ 1927 \div 3 &= 642 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1927 \div 12 = 160 \text{R} 7 \end{equation} So, $160\times 3 = 480$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $480+2=482$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1927 \div 4 &= 481 \text{R} 3 \\ 1927 \div 3 &= 642 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1927 \div 12 = 160 \text{R} 7 \end{equation} So, $160\times 3 = 480$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $480+2=482$
1933 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1933 \div 4 &= 483 \text{R} 1 \\ 1933 \div 3 &= 644 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1933 \div 12 = 161 \text{R} 1 \end{equation} So, $161\times 3 = 483$. But the last soldier had the same number both times. So, $483+1=484$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1933 \div 4 &= 483 \text{R} 1 \\ 1933 \div 3 &= 644 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1933 \div 12 = 161 \text{R} 1 \end{equation} So, $161\times 3 = 483$. But the last soldier had the same number both times. So, $483+1=484$
1939 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1939 \div 4 &= 484 \text{R} 3 \\ 1939 \div 3 &= 646 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1939 \div 12 = 161 \text{R} 7 \end{equation} So, $161\times 3 = 483$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $483+2=485$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1939 \div 4 &= 484 \text{R} 3 \\ 1939 \div 3 &= 646 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1939 \div 12 = 161 \text{R} 7 \end{equation} So, $161\times 3 = 483$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $483+2=485$
1945 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1945 \div 4 &= 486 \text{R} 1 \\ 1945 \div 3 &= 648 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1945 \div 12 = 162 \text{R} 1 \end{equation} So, $162\times 3 = 486$. But the last soldier had the same number both times. So, $486+1=487$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1945 \div 4 &= 486 \text{R} 1 \\ 1945 \div 3 &= 648 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1945 \div 12 = 162 \text{R} 1 \end{equation} So, $162\times 3 = 486$. But the last soldier had the same number both times. So, $486+1=487$
1951 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1951 \div 4 &= 487 \text{R} 3 \\ 1951 \div 3 &= 650 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1951 \div 12 = 162 \text{R} 7 \end{equation} So, $162\times 3 = 486$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $486+2=488$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1951 \div 4 &= 487 \text{R} 3 \\ 1951 \div 3 &= 650 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1951 \div 12 = 162 \text{R} 7 \end{equation} So, $162\times 3 = 486$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $486+2=488$
1957 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1957 \div 4 &= 489 \text{R} 1 \\ 1957 \div 3 &= 652 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1957 \div 12 = 163 \text{R} 1 \end{equation} So, $163\times 3 = 489$. But the last soldier had the same number both times. So, $489+1=490$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1957 \div 4 &= 489 \text{R} 1 \\ 1957 \div 3 &= 652 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1957 \div 12 = 163 \text{R} 1 \end{equation} So, $163\times 3 = 489$. But the last soldier had the same number both times. So, $489+1=490$
1963 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1963 \div 4 &= 490 \text{R} 3 \\ 1963 \div 3 &= 654 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1963 \div 12 = 163 \text{R} 7 \end{equation} So, $163\times 3 = 489$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $489+2=491$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1963 \div 4 &= 490 \text{R} 3 \\ 1963 \div 3 &= 654 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1963 \div 12 = 163 \text{R} 7 \end{equation} So, $163\times 3 = 489$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $489+2=491$
1969 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1969 \div 4 &= 492 \text{R} 1 \\ 1969 \div 3 &= 656 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1969 \div 12 = 164 \text{R} 1 \end{equation} So, $164\times 3 = 492$. But the last soldier had the same number both times. So, $492+1=493$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1969 \div 4 &= 492 \text{R} 1 \\ 1969 \div 3 &= 656 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1969 \div 12 = 164 \text{R} 1 \end{equation} So, $164\times 3 = 492$. But the last soldier had the same number both times. So, $492+1=493$
1975 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1975 \div 4 &= 493 \text{R} 3 \\ 1975 \div 3 &= 658 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1975 \div 12 = 164 \text{R} 7 \end{equation} So, $164\times 3 = 492$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $492+2=494$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1975 \div 4 &= 493 \text{R} 3 \\ 1975 \div 3 &= 658 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1975 \div 12 = 164 \text{R} 7 \end{equation} So, $164\times 3 = 492$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $492+2=494$
1981 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1981 \div 4 &= 495 \text{R} 1 \\ 1981 \div 3 &= 660 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1981 \div 12 = 165 \text{R} 1 \end{equation} So, $165\times 3 = 495$. But the last soldier had the same number both times. So, $495+1=496$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1981 \div 4 &= 495 \text{R} 1 \\ 1981 \div 3 &= 660 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1981 \div 12 = 165 \text{R} 1 \end{equation} So, $165\times 3 = 495$. But the last soldier had the same number both times. So, $495+1=496$
1987 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1987 \div 4 &= 496 \text{R} 3 \\ 1987 \div 3 &= 662 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1987 \div 12 = 165 \text{R} 7 \end{equation} So, $165\times 3 = 495$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $495+2=497$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1987 \div 4 &= 496 \text{R} 3 \\ 1987 \div 3 &= 662 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1987 \div 12 = 165 \text{R} 7 \end{equation} So, $165\times 3 = 495$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $495+2=497$
1993 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1993 \div 4 &= 498 \text{R} 1 \\ 1993 \div 3 &= 664 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1993 \div 12 = 166 \text{R} 1 \end{equation} So, $166\times 3 = 498$. But the last soldier had the same number both times. So, $498+1=499$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1993 \div 4 &= 498 \text{R} 1 \\ 1993 \div 3 &= 664 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1993 \div 12 = 166 \text{R} 1 \end{equation} So, $166\times 3 = 498$. But the last soldier had the same number both times. So, $498+1=499$
1999 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1999 \div 4 &= 499 \text{R} 3 \\ 1999 \div 3 &= 666 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1999 \div 12 = 166 \text{R} 7 \end{equation} So, $166\times 3 = 498$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $498+2=500$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1999 \div 4 &= 499 \text{R} 3 \\ 1999 \div 3 &= 666 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 1999 \div 12 = 166 \text{R} 7 \end{equation} So, $166\times 3 = 498$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $498+2=500$
2005 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2005 \div 4 &= 501 \text{R} 1 \\ 2005 \div 3 &= 668 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2005 \div 12 = 167 \text{R} 1 \end{equation} So, $167\times 3 = 501$. But the last soldier had the same number both times. So, $501+1=502$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2005 \div 4 &= 501 \text{R} 1 \\ 2005 \div 3 &= 668 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2005 \div 12 = 167 \text{R} 1 \end{equation} So, $167\times 3 = 501$. But the last soldier had the same number both times. So, $501+1=502$
2011 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2011 \div 4 &= 502 \text{R} 3 \\ 2011 \div 3 &= 670 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2011 \div 12 = 167 \text{R} 7 \end{equation} So, $167\times 3 = 501$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $501+2=503$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2011 \div 4 &= 502 \text{R} 3 \\ 2011 \div 3 &= 670 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2011 \div 12 = 167 \text{R} 7 \end{equation} So, $167\times 3 = 501$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $501+2=503$
2017 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2017 \div 4 &= 504 \text{R} 1 \\ 2017 \div 3 &= 672 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2017 \div 12 = 168 \text{R} 1 \end{equation} So, $168\times 3 = 504$. But the last soldier had the same number both times. So, $504+1=505$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2017 \div 4 &= 504 \text{R} 1 \\ 2017 \div 3 &= 672 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2017 \div 12 = 168 \text{R} 1 \end{equation} So, $168\times 3 = 504$. But the last soldier had the same number both times. So, $504+1=505$
2023 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2023 \div 4 &= 505 \text{R} 3 \\ 2023 \div 3 &= 674 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2023 \div 12 = 168 \text{R} 7 \end{equation} So, $168\times 3 = 504$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $504+2=506$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2023 \div 4 &= 505 \text{R} 3 \\ 2023 \div 3 &= 674 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2023 \div 12 = 168 \text{R} 7 \end{equation} So, $168\times 3 = 504$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $504+2=506$
2029 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2029 \div 4 &= 507 \text{R} 1 \\ 2029 \div 3 &= 676 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2029 \div 12 = 169 \text{R} 1 \end{equation} So, $169\times 3 = 507$. But the last soldier had the same number both times. So, $507+1=508$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2029 \div 4 &= 507 \text{R} 1 \\ 2029 \div 3 &= 676 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2029 \div 12 = 169 \text{R} 1 \end{equation} So, $169\times 3 = 507$. But the last soldier had the same number both times. So, $507+1=508$
2035 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2035 \div 4 &= 508 \text{R} 3 \\ 2035 \div 3 &= 678 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2035 \div 12 = 169 \text{R} 7 \end{equation} So, $169\times 3 = 507$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $507+2=509$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2035 \div 4 &= 508 \text{R} 3 \\ 2035 \div 3 &= 678 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2035 \div 12 = 169 \text{R} 7 \end{equation} So, $169\times 3 = 507$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $507+2=509$
2041 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2041 \div 4 &= 510 \text{R} 1 \\ 2041 \div 3 &= 680 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2041 \div 12 = 170 \text{R} 1 \end{equation} So, $170\times 3 = 510$. But the last soldier had the same number both times. So, $510+1=511$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2041 \div 4 &= 510 \text{R} 1 \\ 2041 \div 3 &= 680 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2041 \div 12 = 170 \text{R} 1 \end{equation} So, $170\times 3 = 510$. But the last soldier had the same number both times. So, $510+1=511$
2047 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2047 \div 4 &= 511 \text{R} 3 \\ 2047 \div 3 &= 682 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2047 \div 12 = 170 \text{R} 7 \end{equation} So, $170\times 3 = 510$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $510+2=512$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2047 \div 4 &= 511 \text{R} 3 \\ 2047 \div 3 &= 682 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2047 \div 12 = 170 \text{R} 7 \end{equation} So, $170\times 3 = 510$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $510+2=512$
2053 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2053 \div 4 &= 513 \text{R} 1 \\ 2053 \div 3 &= 684 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2053 \div 12 = 171 \text{R} 1 \end{equation} So, $171\times 3 = 513$. But the last soldier had the same number both times. So, $513+1=514$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2053 \div 4 &= 513 \text{R} 1 \\ 2053 \div 3 &= 684 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2053 \div 12 = 171 \text{R} 1 \end{equation} So, $171\times 3 = 513$. But the last soldier had the same number both times. So, $513+1=514$
2059 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2059 \div 4 &= 514 \text{R} 3 \\ 2059 \div 3 &= 686 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2059 \div 12 = 171 \text{R} 7 \end{equation} So, $171\times 3 = 513$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $513+2=515$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2059 \div 4 &= 514 \text{R} 3 \\ 2059 \div 3 &= 686 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2059 \div 12 = 171 \text{R} 7 \end{equation} So, $171\times 3 = 513$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $513+2=515$
2065 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2065 \div 4 &= 516 \text{R} 1 \\ 2065 \div 3 &= 688 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2065 \div 12 = 172 \text{R} 1 \end{equation} So, $172\times 3 = 516$. But the last soldier had the same number both times. So, $516+1=517$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2065 \div 4 &= 516 \text{R} 1 \\ 2065 \div 3 &= 688 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2065 \div 12 = 172 \text{R} 1 \end{equation} So, $172\times 3 = 516$. But the last soldier had the same number both times. So, $516+1=517$
2071 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2071 \div 4 &= 517 \text{R} 3 \\ 2071 \div 3 &= 690 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2071 \div 12 = 172 \text{R} 7 \end{equation} So, $172\times 3 = 516$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $516+2=518$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2071 \div 4 &= 517 \text{R} 3 \\ 2071 \div 3 &= 690 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2071 \div 12 = 172 \text{R} 7 \end{equation} So, $172\times 3 = 516$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $516+2=518$
2077 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2077 \div 4 &= 519 \text{R} 1 \\ 2077 \div 3 &= 692 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2077 \div 12 = 173 \text{R} 1 \end{equation} So, $173\times 3 = 519$. But the last soldier had the same number both times. So, $519+1=520$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2077 \div 4 &= 519 \text{R} 1 \\ 2077 \div 3 &= 692 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2077 \div 12 = 173 \text{R} 1 \end{equation} So, $173\times 3 = 519$. But the last soldier had the same number both times. So, $519+1=520$
2083 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2083 \div 4 &= 520 \text{R} 3 \\ 2083 \div 3 &= 694 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2083 \div 12 = 173 \text{R} 7 \end{equation} So, $173\times 3 = 519$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $519+2=521$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2083 \div 4 &= 520 \text{R} 3 \\ 2083 \div 3 &= 694 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2083 \div 12 = 173 \text{R} 7 \end{equation} So, $173\times 3 = 519$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $519+2=521$
2089 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2089 \div 4 &= 522 \text{R} 1 \\ 2089 \div 3 &= 696 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2089 \div 12 = 174 \text{R} 1 \end{equation} So, $174\times 3 = 522$. But the last soldier had the same number both times. So, $522+1=523$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2089 \div 4 &= 522 \text{R} 1 \\ 2089 \div 3 &= 696 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2089 \div 12 = 174 \text{R} 1 \end{equation} So, $174\times 3 = 522$. But the last soldier had the same number both times. So, $522+1=523$
2095 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2095 \div 4 &= 523 \text{R} 3 \\ 2095 \div 3 &= 698 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2095 \div 12 = 174 \text{R} 7 \end{equation} So, $174\times 3 = 522$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $522+2=524$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2095 \div 4 &= 523 \text{R} 3 \\ 2095 \div 3 &= 698 \text{R} 1 \\ \end{align*} Every 12 soldiers there are 3 with the same numbers. \begin{equation} 2095 \div 12 = 174 \text{R} 7 \end{equation} So, $174\times 3 = 522$. But there are 2 more soldiers with the same numbers in the last 7 soldiers. So, $522+2=524$
1903 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1903 \div 5 &= 380 \text{R} 3 \\ 1903 \div 3 &= 634 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1903 \div 15 = 126 \text{R} 13 \end{equation} So, $126\times 3 = 378$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $378+3=381$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1903 \div 5 &= 380 \text{R} 3 \\ 1903 \div 3 &= 634 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1903 \div 15 = 126 \text{R} 13 \end{equation} So, $126\times 3 = 378$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $378+3=381$
1906 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1906 \div 5 &= 381 \text{R} 1 \\ 1906 \div 3 &= 635 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1906 \div 15 = 127 \text{R} 1 \end{equation} So, $127\times 3 = 381$. But the last soldier had the same number both times. So, $381+1=382$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1906 \div 5 &= 381 \text{R} 1 \\ 1906 \div 3 &= 635 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1906 \div 15 = 127 \text{R} 1 \end{equation} So, $127\times 3 = 381$. But the last soldier had the same number both times. So, $381+1=382$
1909 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1909 \div 5 &= 381 \text{R} 4 \\ 1909 \div 3 &= 636 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1909 \div 15 = 127 \text{R} 4 \end{equation} So, $127\times 3 = 381$. But the last soldier had the same number both times. So, $381+1=382$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1909 \div 5 &= 381 \text{R} 4 \\ 1909 \div 3 &= 636 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1909 \div 15 = 127 \text{R} 4 \end{equation} So, $127\times 3 = 381$. But the last soldier had the same number both times. So, $381+1=382$
1918 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1918 \div 5 &= 383 \text{R} 3 \\ 1918 \div 3 &= 639 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1918 \div 15 = 127 \text{R} 13 \end{equation} So, $127\times 3 = 381$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $381+3=384$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1918 \div 5 &= 383 \text{R} 3 \\ 1918 \div 3 &= 639 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1918 \div 15 = 127 \text{R} 13 \end{equation} So, $127\times 3 = 381$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $381+3=384$
1921 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1921 \div 5 &= 384 \text{R} 1 \\ 1921 \div 3 &= 640 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1921 \div 15 = 128 \text{R} 1 \end{equation} So, $128\times 3 = 384$. But the last soldier had the same number both times. So, $384+1=385$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1921 \div 5 &= 384 \text{R} 1 \\ 1921 \div 3 &= 640 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1921 \div 15 = 128 \text{R} 1 \end{equation} So, $128\times 3 = 384$. But the last soldier had the same number both times. So, $384+1=385$
1924 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1924 \div 5 &= 384 \text{R} 4 \\ 1924 \div 3 &= 641 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1924 \div 15 = 128 \text{R} 4 \end{equation} So, $128\times 3 = 384$. But the last soldier had the same number both times. So, $384+1=385$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1924 \div 5 &= 384 \text{R} 4 \\ 1924 \div 3 &= 641 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1924 \div 15 = 128 \text{R} 4 \end{equation} So, $128\times 3 = 384$. But the last soldier had the same number both times. So, $384+1=385$
1933 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1933 \div 5 &= 386 \text{R} 3 \\ 1933 \div 3 &= 644 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1933 \div 15 = 128 \text{R} 13 \end{equation} So, $128\times 3 = 384$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $384+3=387$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1933 \div 5 &= 386 \text{R} 3 \\ 1933 \div 3 &= 644 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1933 \div 15 = 128 \text{R} 13 \end{equation} So, $128\times 3 = 384$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $384+3=387$
1936 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1936 \div 5 &= 387 \text{R} 1 \\ 1936 \div 3 &= 645 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1936 \div 15 = 129 \text{R} 1 \end{equation} So, $129\times 3 = 387$. But the last soldier had the same number both times. So, $387+1=388$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1936 \div 5 &= 387 \text{R} 1 \\ 1936 \div 3 &= 645 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1936 \div 15 = 129 \text{R} 1 \end{equation} So, $129\times 3 = 387$. But the last soldier had the same number both times. So, $387+1=388$
1939 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1939 \div 5 &= 387 \text{R} 4 \\ 1939 \div 3 &= 646 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1939 \div 15 = 129 \text{R} 4 \end{equation} So, $129\times 3 = 387$. But the last soldier had the same number both times. So, $387+1=388$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1939 \div 5 &= 387 \text{R} 4 \\ 1939 \div 3 &= 646 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1939 \div 15 = 129 \text{R} 4 \end{equation} So, $129\times 3 = 387$. But the last soldier had the same number both times. So, $387+1=388$
1948 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1948 \div 5 &= 389 \text{R} 3 \\ 1948 \div 3 &= 649 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1948 \div 15 = 129 \text{R} 13 \end{equation} So, $129\times 3 = 387$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $387+3=390$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1948 \div 5 &= 389 \text{R} 3 \\ 1948 \div 3 &= 649 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1948 \div 15 = 129 \text{R} 13 \end{equation} So, $129\times 3 = 387$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $387+3=390$
1951 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1951 \div 5 &= 390 \text{R} 1 \\ 1951 \div 3 &= 650 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1951 \div 15 = 130 \text{R} 1 \end{equation} So, $130\times 3 = 390$. But the last soldier had the same number both times. So, $390+1=391$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1951 \div 5 &= 390 \text{R} 1 \\ 1951 \div 3 &= 650 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1951 \div 15 = 130 \text{R} 1 \end{equation} So, $130\times 3 = 390$. But the last soldier had the same number both times. So, $390+1=391$
1954 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1954 \div 5 &= 390 \text{R} 4 \\ 1954 \div 3 &= 651 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1954 \div 15 = 130 \text{R} 4 \end{equation} So, $130\times 3 = 390$. But the last soldier had the same number both times. So, $390+1=391$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1954 \div 5 &= 390 \text{R} 4 \\ 1954 \div 3 &= 651 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1954 \div 15 = 130 \text{R} 4 \end{equation} So, $130\times 3 = 390$. But the last soldier had the same number both times. So, $390+1=391$
1963 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1963 \div 5 &= 392 \text{R} 3 \\ 1963 \div 3 &= 654 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1963 \div 15 = 130 \text{R} 13 \end{equation} So, $130\times 3 = 390$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $390+3=393$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1963 \div 5 &= 392 \text{R} 3 \\ 1963 \div 3 &= 654 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1963 \div 15 = 130 \text{R} 13 \end{equation} So, $130\times 3 = 390$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $390+3=393$
1966 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1966 \div 5 &= 393 \text{R} 1 \\ 1966 \div 3 &= 655 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1966 \div 15 = 131 \text{R} 1 \end{equation} So, $131\times 3 = 393$. But the last soldier had the same number both times. So, $393+1=394$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1966 \div 5 &= 393 \text{R} 1 \\ 1966 \div 3 &= 655 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1966 \div 15 = 131 \text{R} 1 \end{equation} So, $131\times 3 = 393$. But the last soldier had the same number both times. So, $393+1=394$
1969 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1969 \div 5 &= 393 \text{R} 4 \\ 1969 \div 3 &= 656 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1969 \div 15 = 131 \text{R} 4 \end{equation} So, $131\times 3 = 393$. But the last soldier had the same number both times. So, $393+1=394$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1969 \div 5 &= 393 \text{R} 4 \\ 1969 \div 3 &= 656 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1969 \div 15 = 131 \text{R} 4 \end{equation} So, $131\times 3 = 393$. But the last soldier had the same number both times. So, $393+1=394$
1978 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1978 \div 5 &= 395 \text{R} 3 \\ 1978 \div 3 &= 659 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1978 \div 15 = 131 \text{R} 13 \end{equation} So, $131\times 3 = 393$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $393+3=396$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1978 \div 5 &= 395 \text{R} 3 \\ 1978 \div 3 &= 659 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1978 \div 15 = 131 \text{R} 13 \end{equation} So, $131\times 3 = 393$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $393+3=396$
1981 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1981 \div 5 &= 396 \text{R} 1 \\ 1981 \div 3 &= 660 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1981 \div 15 = 132 \text{R} 1 \end{equation} So, $132\times 3 = 396$. But the last soldier had the same number both times. So, $396+1=397$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1981 \div 5 &= 396 \text{R} 1 \\ 1981 \div 3 &= 660 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1981 \div 15 = 132 \text{R} 1 \end{equation} So, $132\times 3 = 396$. But the last soldier had the same number both times. So, $396+1=397$
1984 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1984 \div 5 &= 396 \text{R} 4 \\ 1984 \div 3 &= 661 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1984 \div 15 = 132 \text{R} 4 \end{equation} So, $132\times 3 = 396$. But the last soldier had the same number both times. So, $396+1=397$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1984 \div 5 &= 396 \text{R} 4 \\ 1984 \div 3 &= 661 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1984 \div 15 = 132 \text{R} 4 \end{equation} So, $132\times 3 = 396$. But the last soldier had the same number both times. So, $396+1=397$
1993 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1993 \div 5 &= 398 \text{R} 3 \\ 1993 \div 3 &= 664 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1993 \div 15 = 132 \text{R} 13 \end{equation} So, $132\times 3 = 396$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $396+3=399$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1993 \div 5 &= 398 \text{R} 3 \\ 1993 \div 3 &= 664 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1993 \div 15 = 132 \text{R} 13 \end{equation} So, $132\times 3 = 396$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $396+3=399$
1996 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1996 \div 5 &= 399 \text{R} 1 \\ 1996 \div 3 &= 665 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1996 \div 15 = 133 \text{R} 1 \end{equation} So, $133\times 3 = 399$. But the last soldier had the same number both times. So, $399+1=400$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1996 \div 5 &= 399 \text{R} 1 \\ 1996 \div 3 &= 665 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1996 \div 15 = 133 \text{R} 1 \end{equation} So, $133\times 3 = 399$. But the last soldier had the same number both times. So, $399+1=400$
1999 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1999 \div 5 &= 399 \text{R} 4 \\ 1999 \div 3 &= 666 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1999 \div 15 = 133 \text{R} 4 \end{equation} So, $133\times 3 = 399$. But the last soldier had the same number both times. So, $399+1=400$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1999 \div 5 &= 399 \text{R} 4 \\ 1999 \div 3 &= 666 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 1999 \div 15 = 133 \text{R} 4 \end{equation} So, $133\times 3 = 399$. But the last soldier had the same number both times. So, $399+1=400$
2008 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2008 \div 5 &= 401 \text{R} 3 \\ 2008 \div 3 &= 669 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2008 \div 15 = 133 \text{R} 13 \end{equation} So, $133\times 3 = 399$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $399+3=402$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2008 \div 5 &= 401 \text{R} 3 \\ 2008 \div 3 &= 669 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2008 \div 15 = 133 \text{R} 13 \end{equation} So, $133\times 3 = 399$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $399+3=402$
2011 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2011 \div 5 &= 402 \text{R} 1 \\ 2011 \div 3 &= 670 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2011 \div 15 = 134 \text{R} 1 \end{equation} So, $134\times 3 = 402$. But the last soldier had the same number both times. So, $402+1=403$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2011 \div 5 &= 402 \text{R} 1 \\ 2011 \div 3 &= 670 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2011 \div 15 = 134 \text{R} 1 \end{equation} So, $134\times 3 = 402$. But the last soldier had the same number both times. So, $402+1=403$
2014 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2014 \div 5 &= 402 \text{R} 4 \\ 2014 \div 3 &= 671 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2014 \div 15 = 134 \text{R} 4 \end{equation} So, $134\times 3 = 402$. But the last soldier had the same number both times. So, $402+1=403$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2014 \div 5 &= 402 \text{R} 4 \\ 2014 \div 3 &= 671 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2014 \div 15 = 134 \text{R} 4 \end{equation} So, $134\times 3 = 402$. But the last soldier had the same number both times. So, $402+1=403$
2023 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2023 \div 5 &= 404 \text{R} 3 \\ 2023 \div 3 &= 674 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2023 \div 15 = 134 \text{R} 13 \end{equation} So, $134\times 3 = 402$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $402+3=405$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2023 \div 5 &= 404 \text{R} 3 \\ 2023 \div 3 &= 674 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2023 \div 15 = 134 \text{R} 13 \end{equation} So, $134\times 3 = 402$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $402+3=405$
2026 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2026 \div 5 &= 405 \text{R} 1 \\ 2026 \div 3 &= 675 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2026 \div 15 = 135 \text{R} 1 \end{equation} So, $135\times 3 = 405$. But the last soldier had the same number both times. So, $405+1=406$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2026 \div 5 &= 405 \text{R} 1 \\ 2026 \div 3 &= 675 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2026 \div 15 = 135 \text{R} 1 \end{equation} So, $135\times 3 = 405$. But the last soldier had the same number both times. So, $405+1=406$
2029 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2029 \div 5 &= 405 \text{R} 4 \\ 2029 \div 3 &= 676 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2029 \div 15 = 135 \text{R} 4 \end{equation} So, $135\times 3 = 405$. But the last soldier had the same number both times. So, $405+1=406$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2029 \div 5 &= 405 \text{R} 4 \\ 2029 \div 3 &= 676 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2029 \div 15 = 135 \text{R} 4 \end{equation} So, $135\times 3 = 405$. But the last soldier had the same number both times. So, $405+1=406$
2038 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2038 \div 5 &= 407 \text{R} 3 \\ 2038 \div 3 &= 679 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2038 \div 15 = 135 \text{R} 13 \end{equation} So, $135\times 3 = 405$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $405+3=408$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2038 \div 5 &= 407 \text{R} 3 \\ 2038 \div 3 &= 679 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2038 \div 15 = 135 \text{R} 13 \end{equation} So, $135\times 3 = 405$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $405+3=408$
2041 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2041 \div 5 &= 408 \text{R} 1 \\ 2041 \div 3 &= 680 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2041 \div 15 = 136 \text{R} 1 \end{equation} So, $136\times 3 = 408$. But the last soldier had the same number both times. So, $408+1=409$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2041 \div 5 &= 408 \text{R} 1 \\ 2041 \div 3 &= 680 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2041 \div 15 = 136 \text{R} 1 \end{equation} So, $136\times 3 = 408$. But the last soldier had the same number both times. So, $408+1=409$
2044 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2044 \div 5 &= 408 \text{R} 4 \\ 2044 \div 3 &= 681 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2044 \div 15 = 136 \text{R} 4 \end{equation} So, $136\times 3 = 408$. But the last soldier had the same number both times. So, $408+1=409$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2044 \div 5 &= 408 \text{R} 4 \\ 2044 \div 3 &= 681 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2044 \div 15 = 136 \text{R} 4 \end{equation} So, $136\times 3 = 408$. But the last soldier had the same number both times. So, $408+1=409$
2053 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2053 \div 5 &= 410 \text{R} 3 \\ 2053 \div 3 &= 684 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2053 \div 15 = 136 \text{R} 13 \end{equation} So, $136\times 3 = 408$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $408+3=411$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2053 \div 5 &= 410 \text{R} 3 \\ 2053 \div 3 &= 684 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2053 \div 15 = 136 \text{R} 13 \end{equation} So, $136\times 3 = 408$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $408+3=411$
2056 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2056 \div 5 &= 411 \text{R} 1 \\ 2056 \div 3 &= 685 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2056 \div 15 = 137 \text{R} 1 \end{equation} So, $137\times 3 = 411$. But the last soldier had the same number both times. So, $411+1=412$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2056 \div 5 &= 411 \text{R} 1 \\ 2056 \div 3 &= 685 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2056 \div 15 = 137 \text{R} 1 \end{equation} So, $137\times 3 = 411$. But the last soldier had the same number both times. So, $411+1=412$
2059 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2059 \div 5 &= 411 \text{R} 4 \\ 2059 \div 3 &= 686 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2059 \div 15 = 137 \text{R} 4 \end{equation} So, $137\times 3 = 411$. But the last soldier had the same number both times. So, $411+1=412$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2059 \div 5 &= 411 \text{R} 4 \\ 2059 \div 3 &= 686 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2059 \div 15 = 137 \text{R} 4 \end{equation} So, $137\times 3 = 411$. But the last soldier had the same number both times. So, $411+1=412$
2068 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2068 \div 5 &= 413 \text{R} 3 \\ 2068 \div 3 &= 689 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2068 \div 15 = 137 \text{R} 13 \end{equation} So, $137\times 3 = 411$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $411+3=414$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2068 \div 5 &= 413 \text{R} 3 \\ 2068 \div 3 &= 689 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2068 \div 15 = 137 \text{R} 13 \end{equation} So, $137\times 3 = 411$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $411+3=414$
2071 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2071 \div 5 &= 414 \text{R} 1 \\ 2071 \div 3 &= 690 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2071 \div 15 = 138 \text{R} 1 \end{equation} So, $138\times 3 = 414$. But the last soldier had the same number both times. So, $414+1=415$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2071 \div 5 &= 414 \text{R} 1 \\ 2071 \div 3 &= 690 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2071 \div 15 = 138 \text{R} 1 \end{equation} So, $138\times 3 = 414$. But the last soldier had the same number both times. So, $414+1=415$
2074 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2074 \div 5 &= 414 \text{R} 4 \\ 2074 \div 3 &= 691 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2074 \div 15 = 138 \text{R} 4 \end{equation} So, $138\times 3 = 414$. But the last soldier had the same number both times. So, $414+1=415$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2074 \div 5 &= 414 \text{R} 4 \\ 2074 \div 3 &= 691 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2074 \div 15 = 138 \text{R} 4 \end{equation} So, $138\times 3 = 414$. But the last soldier had the same number both times. So, $414+1=415$
2083 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2083 \div 5 &= 416 \text{R} 3 \\ 2083 \div 3 &= 694 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2083 \div 15 = 138 \text{R} 13 \end{equation} So, $138\times 3 = 414$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $414+3=417$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2083 \div 5 &= 416 \text{R} 3 \\ 2083 \div 3 &= 694 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2083 \div 15 = 138 \text{R} 13 \end{equation} So, $138\times 3 = 414$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $414+3=417$
2086 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2086 \div 5 &= 417 \text{R} 1 \\ 2086 \div 3 &= 695 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2086 \div 15 = 139 \text{R} 1 \end{equation} So, $139\times 3 = 417$. But the last soldier had the same number both times. So, $417+1=418$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2086 \div 5 &= 417 \text{R} 1 \\ 2086 \div 3 &= 695 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2086 \div 15 = 139 \text{R} 1 \end{equation} So, $139\times 3 = 417$. But the last soldier had the same number both times. So, $417+1=418$
2089 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2089 \div 5 &= 417 \text{R} 4 \\ 2089 \div 3 &= 696 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2089 \div 15 = 139 \text{R} 4 \end{equation} So, $139\times 3 = 417$. But the last soldier had the same number both times. So, $417+1=418$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2089 \div 5 &= 417 \text{R} 4 \\ 2089 \div 3 &= 696 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2089 \div 15 = 139 \text{R} 4 \end{equation} So, $139\times 3 = 417$. But the last soldier had the same number both times. So, $417+1=418$
2098 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 1, 2, 3, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2098 \div 5 &= 419 \text{R} 3 \\ 2098 \div 3 &= 699 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2098 \div 15 = 139 \text{R} 13 \end{equation} So, $139\times 3 = 417$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $417+3=420$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2098 \div 5 &= 419 \text{R} 3 \\ 2098 \div 3 &= 699 \text{R} 1 \\ \end{align*} Every 15 soldiers there are 3 with the same numbers. \begin{equation} 2098 \div 15 = 139 \text{R} 13 \end{equation} So, $139\times 3 = 417$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $417+3=420$
1901 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1901 \div 5 &= 380 \text{R} 1 \\ 1901 \div 4 &= 475 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1901 \div 20 = 95 \text{R} 1 \end{equation} So, $95\times 4 = 380$. But the last soldier had the same number both times. So, $380+1=381$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1901 \div 5 &= 380 \text{R} 1 \\ 1901 \div 4 &= 475 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1901 \div 20 = 95 \text{R} 1 \end{equation} So, $95\times 4 = 380$. But the last soldier had the same number both times. So, $380+1=381$
1905 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1905 \div 5 &= 381 \text{R} 0 \\ 1905 \div 4 &= 476 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1905 \div 20 = 95 \text{R} 5 \end{equation} So, $95\times 4 = 380$. But there are 2 more soldiers with the same numbers in the last 5 soldiers. So, $380+2=382$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1905 \div 5 &= 381 \text{R} 0 \\ 1905 \div 4 &= 476 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1905 \div 20 = 95 \text{R} 5 \end{equation} So, $95\times 4 = 380$. But there are 2 more soldiers with the same numbers in the last 5 soldiers. So, $380+2=382$
1909 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1909 \div 5 &= 381 \text{R} 4 \\ 1909 \div 4 &= 477 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1909 \div 20 = 95 \text{R} 9 \end{equation} So, $95\times 4 = 380$. But there are 2 more soldiers with the same numbers in the last 9 soldiers. So, $380+2=382$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1909 \div 5 &= 381 \text{R} 4 \\ 1909 \div 4 &= 477 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1909 \div 20 = 95 \text{R} 9 \end{equation} So, $95\times 4 = 380$. But there are 2 more soldiers with the same numbers in the last 9 soldiers. So, $380+2=382$
1913 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1913 \div 5 &= 382 \text{R} 3 \\ 1913 \div 4 &= 478 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1913 \div 20 = 95 \text{R} 13 \end{equation} So, $95\times 4 = 380$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $380+3=383$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1913 \div 5 &= 382 \text{R} 3 \\ 1913 \div 4 &= 478 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1913 \div 20 = 95 \text{R} 13 \end{equation} So, $95\times 4 = 380$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $380+3=383$
1917 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1917 \div 5 &= 383 \text{R} 2 \\ 1917 \div 4 &= 479 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1917 \div 20 = 95 \text{R} 17 \end{equation} So, $95\times 4 = 380$. But there are 4 more soldiers with the same numbers in the last 17 soldiers. So, $380+4=384$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1917 \div 5 &= 383 \text{R} 2 \\ 1917 \div 4 &= 479 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1917 \div 20 = 95 \text{R} 17 \end{equation} So, $95\times 4 = 380$. But there are 4 more soldiers with the same numbers in the last 17 soldiers. So, $380+4=384$
1921 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1921 \div 5 &= 384 \text{R} 1 \\ 1921 \div 4 &= 480 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1921 \div 20 = 96 \text{R} 1 \end{equation} So, $96\times 4 = 384$. But the last soldier had the same number both times. So, $384+1=385$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1921 \div 5 &= 384 \text{R} 1 \\ 1921 \div 4 &= 480 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1921 \div 20 = 96 \text{R} 1 \end{equation} So, $96\times 4 = 384$. But the last soldier had the same number both times. So, $384+1=385$
1925 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1925 \div 5 &= 385 \text{R} 0 \\ 1925 \div 4 &= 481 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1925 \div 20 = 96 \text{R} 5 \end{equation} So, $96\times 4 = 384$. But there are 2 more soldiers with the same numbers in the last 5 soldiers. So, $384+2=386$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1925 \div 5 &= 385 \text{R} 0 \\ 1925 \div 4 &= 481 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1925 \div 20 = 96 \text{R} 5 \end{equation} So, $96\times 4 = 384$. But there are 2 more soldiers with the same numbers in the last 5 soldiers. So, $384+2=386$
1929 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1929 \div 5 &= 385 \text{R} 4 \\ 1929 \div 4 &= 482 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1929 \div 20 = 96 \text{R} 9 \end{equation} So, $96\times 4 = 384$. But there are 2 more soldiers with the same numbers in the last 9 soldiers. So, $384+2=386$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1929 \div 5 &= 385 \text{R} 4 \\ 1929 \div 4 &= 482 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1929 \div 20 = 96 \text{R} 9 \end{equation} So, $96\times 4 = 384$. But there are 2 more soldiers with the same numbers in the last 9 soldiers. So, $384+2=386$
1933 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1933 \div 5 &= 386 \text{R} 3 \\ 1933 \div 4 &= 483 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1933 \div 20 = 96 \text{R} 13 \end{equation} So, $96\times 4 = 384$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $384+3=387$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1933 \div 5 &= 386 \text{R} 3 \\ 1933 \div 4 &= 483 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1933 \div 20 = 96 \text{R} 13 \end{equation} So, $96\times 4 = 384$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $384+3=387$
1937 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1937 \div 5 &= 387 \text{R} 2 \\ 1937 \div 4 &= 484 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1937 \div 20 = 96 \text{R} 17 \end{equation} So, $96\times 4 = 384$. But there are 4 more soldiers with the same numbers in the last 17 soldiers. So, $384+4=388$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1937 \div 5 &= 387 \text{R} 2 \\ 1937 \div 4 &= 484 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1937 \div 20 = 96 \text{R} 17 \end{equation} So, $96\times 4 = 384$. But there are 4 more soldiers with the same numbers in the last 17 soldiers. So, $384+4=388$
1941 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1941 \div 5 &= 388 \text{R} 1 \\ 1941 \div 4 &= 485 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1941 \div 20 = 97 \text{R} 1 \end{equation} So, $97\times 4 = 388$. But the last soldier had the same number both times. So, $388+1=389$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1941 \div 5 &= 388 \text{R} 1 \\ 1941 \div 4 &= 485 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1941 \div 20 = 97 \text{R} 1 \end{equation} So, $97\times 4 = 388$. But the last soldier had the same number both times. So, $388+1=389$
1945 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1945 \div 5 &= 389 \text{R} 0 \\ 1945 \div 4 &= 486 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1945 \div 20 = 97 \text{R} 5 \end{equation} So, $97\times 4 = 388$. But there are 2 more soldiers with the same numbers in the last 5 soldiers. So, $388+2=390$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1945 \div 5 &= 389 \text{R} 0 \\ 1945 \div 4 &= 486 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1945 \div 20 = 97 \text{R} 5 \end{equation} So, $97\times 4 = 388$. But there are 2 more soldiers with the same numbers in the last 5 soldiers. So, $388+2=390$
1949 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1949 \div 5 &= 389 \text{R} 4 \\ 1949 \div 4 &= 487 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1949 \div 20 = 97 \text{R} 9 \end{equation} So, $97\times 4 = 388$. But there are 2 more soldiers with the same numbers in the last 9 soldiers. So, $388+2=390$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1949 \div 5 &= 389 \text{R} 4 \\ 1949 \div 4 &= 487 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1949 \div 20 = 97 \text{R} 9 \end{equation} So, $97\times 4 = 388$. But there are 2 more soldiers with the same numbers in the last 9 soldiers. So, $388+2=390$
1953 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1953 \div 5 &= 390 \text{R} 3 \\ 1953 \div 4 &= 488 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1953 \div 20 = 97 \text{R} 13 \end{equation} So, $97\times 4 = 388$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $388+3=391$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1953 \div 5 &= 390 \text{R} 3 \\ 1953 \div 4 &= 488 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1953 \div 20 = 97 \text{R} 13 \end{equation} So, $97\times 4 = 388$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $388+3=391$
1957 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1957 \div 5 &= 391 \text{R} 2 \\ 1957 \div 4 &= 489 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1957 \div 20 = 97 \text{R} 17 \end{equation} So, $97\times 4 = 388$. But there are 4 more soldiers with the same numbers in the last 17 soldiers. So, $388+4=392$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1957 \div 5 &= 391 \text{R} 2 \\ 1957 \div 4 &= 489 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1957 \div 20 = 97 \text{R} 17 \end{equation} So, $97\times 4 = 388$. But there are 4 more soldiers with the same numbers in the last 17 soldiers. So, $388+4=392$
1961 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1961 \div 5 &= 392 \text{R} 1 \\ 1961 \div 4 &= 490 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1961 \div 20 = 98 \text{R} 1 \end{equation} So, $98\times 4 = 392$. But the last soldier had the same number both times. So, $392+1=393$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1961 \div 5 &= 392 \text{R} 1 \\ 1961 \div 4 &= 490 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1961 \div 20 = 98 \text{R} 1 \end{equation} So, $98\times 4 = 392$. But the last soldier had the same number both times. So, $392+1=393$
1965 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1965 \div 5 &= 393 \text{R} 0 \\ 1965 \div 4 &= 491 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1965 \div 20 = 98 \text{R} 5 \end{equation} So, $98\times 4 = 392$. But there are 2 more soldiers with the same numbers in the last 5 soldiers. So, $392+2=394$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1965 \div 5 &= 393 \text{R} 0 \\ 1965 \div 4 &= 491 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1965 \div 20 = 98 \text{R} 5 \end{equation} So, $98\times 4 = 392$. But there are 2 more soldiers with the same numbers in the last 5 soldiers. So, $392+2=394$
1969 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1969 \div 5 &= 393 \text{R} 4 \\ 1969 \div 4 &= 492 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1969 \div 20 = 98 \text{R} 9 \end{equation} So, $98\times 4 = 392$. But there are 2 more soldiers with the same numbers in the last 9 soldiers. So, $392+2=394$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1969 \div 5 &= 393 \text{R} 4 \\ 1969 \div 4 &= 492 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1969 \div 20 = 98 \text{R} 9 \end{equation} So, $98\times 4 = 392$. But there are 2 more soldiers with the same numbers in the last 9 soldiers. So, $392+2=394$
1973 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1973 \div 5 &= 394 \text{R} 3 \\ 1973 \div 4 &= 493 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1973 \div 20 = 98 \text{R} 13 \end{equation} So, $98\times 4 = 392$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $392+3=395$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1973 \div 5 &= 394 \text{R} 3 \\ 1973 \div 4 &= 493 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1973 \div 20 = 98 \text{R} 13 \end{equation} So, $98\times 4 = 392$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $392+3=395$
1977 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1977 \div 5 &= 395 \text{R} 2 \\ 1977 \div 4 &= 494 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1977 \div 20 = 98 \text{R} 17 \end{equation} So, $98\times 4 = 392$. But there are 4 more soldiers with the same numbers in the last 17 soldiers. So, $392+4=396$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1977 \div 5 &= 395 \text{R} 2 \\ 1977 \div 4 &= 494 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1977 \div 20 = 98 \text{R} 17 \end{equation} So, $98\times 4 = 392$. But there are 4 more soldiers with the same numbers in the last 17 soldiers. So, $392+4=396$
1981 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1981 \div 5 &= 396 \text{R} 1 \\ 1981 \div 4 &= 495 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1981 \div 20 = 99 \text{R} 1 \end{equation} So, $99\times 4 = 396$. But the last soldier had the same number both times. So, $396+1=397$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1981 \div 5 &= 396 \text{R} 1 \\ 1981 \div 4 &= 495 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1981 \div 20 = 99 \text{R} 1 \end{equation} So, $99\times 4 = 396$. But the last soldier had the same number both times. So, $396+1=397$
1985 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1985 \div 5 &= 397 \text{R} 0 \\ 1985 \div 4 &= 496 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1985 \div 20 = 99 \text{R} 5 \end{equation} So, $99\times 4 = 396$. But there are 2 more soldiers with the same numbers in the last 5 soldiers. So, $396+2=398$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1985 \div 5 &= 397 \text{R} 0 \\ 1985 \div 4 &= 496 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1985 \div 20 = 99 \text{R} 5 \end{equation} So, $99\times 4 = 396$. But there are 2 more soldiers with the same numbers in the last 5 soldiers. So, $396+2=398$
1989 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1989 \div 5 &= 397 \text{R} 4 \\ 1989 \div 4 &= 497 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1989 \div 20 = 99 \text{R} 9 \end{equation} So, $99\times 4 = 396$. But there are 2 more soldiers with the same numbers in the last 9 soldiers. So, $396+2=398$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1989 \div 5 &= 397 \text{R} 4 \\ 1989 \div 4 &= 497 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1989 \div 20 = 99 \text{R} 9 \end{equation} So, $99\times 4 = 396$. But there are 2 more soldiers with the same numbers in the last 9 soldiers. So, $396+2=398$
1993 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1993 \div 5 &= 398 \text{R} 3 \\ 1993 \div 4 &= 498 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1993 \div 20 = 99 \text{R} 13 \end{equation} So, $99\times 4 = 396$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $396+3=399$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1993 \div 5 &= 398 \text{R} 3 \\ 1993 \div 4 &= 498 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1993 \div 20 = 99 \text{R} 13 \end{equation} So, $99\times 4 = 396$. But there are 3 more soldiers with the same numbers in the last 13 soldiers. So, $396+3=399$
1997 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1997 \div 5 &= 399 \text{R} 2 \\ 1997 \div 4 &= 499 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1997 \div 20 = 99 \text{R} 17 \end{equation} So, $99\times 4 = 396$. But there are 4 more soldiers with the same numbers in the last 17 soldiers. So, $396+4=400$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 1997 \div 5 &= 399 \text{R} 2 \\ 1997 \div 4 &= 499 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 1997 \div 20 = 99 \text{R} 17 \end{equation} So, $99\times 4 = 396$. But there are 4 more soldiers with the same numbers in the last 17 soldiers. So, $396+4=400$
2001 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2001 \div 5 &= 400 \text{R} 1 \\ 2001 \div 4 &= 500 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 2001 \div 20 = 100 \text{R} 1 \end{equation} So, $100\times 4 = 400$. But the last soldier had the same number both times. So, $400+1=401$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2001 \div 5 &= 400 \text{R} 1 \\ 2001 \div 4 &= 500 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 2001 \div 20 = 100 \text{R} 1 \end{equation} So, $100\times 4 = 400$. But the last soldier had the same number both times. So, $400+1=401$
2005 soldiers were lined up in a single file. The commander ordered them to number off 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, $\dots$ starting from the first soldier. He then ordered them to number off 1, 2, 3, 4, 1, 2, 3, 4, $\dots$ starting from the last soldier. How many soldiers had the same number both times?
Select An Answer
Sorry. Please check the correct answer below.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2005 \div 5 &= 401 \text{R} 0 \\ 2005 \div 4 &= 501 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 2005 \div 20 = 100 \text{R} 5 \end{equation} So, $100\times 4 = 400$. But there are 2 more soldiers with the same numbers in the last 5 soldiers. So, $400+2=402$
Yay! Your are right.
Consider the following table where the first row stands for the first numbering of the soldiers \begin{equation} \begin{array}{*{15}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 \\ \hline 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 \end{array} \end{equation} \begin{equation} \begin{array}{*{13}{|c}|c|} 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & 4 & 5 & 1 & 2 & 3 & \cdots \\ \hline 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & 1 & 4 & 3 & 2 & \cdots \end{array} \end{equation} \begin{align*} 2005 \div 5 &= 401 \text{R} 0 \\ 2005 \div 4 &= 501 \text{R} 1 \\ \end{align*} Every 20 soldiers there are 4 with the same numbers. \begin{equation} 2005 \div 20 = 100 \text{R} 5 \end{equation} So, $100\times 4 = 400$. But there are 2 more soldiers with the same numbers in the last 5 soldiers. So, $400+2=402$
General
2025 © All Rights Reserved. Privacy Policy | Terms of Service
What subject area do you need help in?
Select level
Select subject


